上官呆呆的笔记

Appearance

概率论 ​

随机事件及其运算 ​

随机事件间的关系与运算 ​

事件关系 ​

事件有三种关系：或，且，对立

A发生必然导致B发生 ​

A发生必然导致B发生
==> A小，B大，B包含A ==>
==>
==> ==>

A与B独立 ​

A与B独立
<==>
<==> 与与与独立

【结论1】
任何事件与概率为0或为1的事件独立
【证明】
（1）与都独立
且
==>
==>

（2）与都独立
与独立与独立

【结论2】
若，则A与B独立
<==>
<==>
<==>
<==>

【结论3】
若，则A与B，独立必不互斥，互斥必不独立
【证明】
A与B互斥 ==> ==> A与B不独立
A与B独立 ==>

减法公式 ​

加法公式 ​

摩根定律 ​

事件对偶律也称为摩根律
摩根律有两个式子，第一个式子的含义：“不会发生A事件或B事件"等价于”A事件和B事件都不会发生“。第二个式子的含义：“A事件和B事件不会同时发生"等价于”A事件不发生或B事件不会发生“概率论中的事件相当于集合论中的集合，事件的加法相当于集合的并，事件的乘法相当于集合的交、集合论中的对偶律（又称德摩根律）。

有限可加性 ​

有限可加性（所有互斥的情况，概率相加）
若互斥
则

【例题】

【例题2】

,

条件概率 ​

条件概率的本质是缩减样本空间

分布 ​

概率密度与分布函数 ​

概率密度函数：

分布函数：
分布函数的性质与判定

分布函数 的性质

性质一： 是一个不减的非负函数（递增）（不是严格递增）

性质二：，，其中 ，

性质三： 即 是右连续的，其中

下列函数中,为某随机变量X的分布函数的是().

(A)

(B)

(C)

(D)

点击展开答案

(B)(C)不满足性质二
(A)不满足性质三

设连续型随机变量X的分布函数为F(x)，且F(0)=0，则下列函数可作为分布函数的是
A.
B.
C.
D.

点击展开答案

(A)可能大于1
(C)不满足性质一
(B)1处不满足右连续

二项分布 ​

二项分布

（1）定义：n重伯努利试验中，A发生的概率为p，那么A发生k次的概率为，
将A发生的次数，设为随机变量X，则，称

（2）考察标志：有xx次A发生的概率 / A发生xx次的概率
==> 次独立重复试验每次相同，试验观察是否发生研究发生的次数

（3）做题步骤：先令试验观察的事件为A，再 令A发生的次数为X，则

泊松分布 ​

泊松分布

（1）

（2）参数可加性
设是相互独立的随机变量且
则

（3）泊松定理（二项分布的极限分布）
足够小足够大

（4）泊松定理应用

【例题】设总体 服从参数为 的泊松分布, 为来自总体 的简单随机样本, 为样本均值, 且 , 则 .

(A)

(B)

(C)

(D)

点击展开答案

解 由于样本方差 , 所以

又 , 由题意 , 得 .
又由 , 所以 相互独立, 且 , 故 , 即 .
记 . 因此 , , 从而

故选 (D).

几何分布 ​

几何分布

（1）定义：做伯努利试验，每次试验中A发生概率为p，一直做到A首次发生时停止，
此时，试验的点次数X，
称试验的点次数X服从几何分布

（2）考察标志：一旦A发生，试验就停止

（3）做题步骤：令A，，A发生时，试验点次数X，则

指数分布 ​

指数分布

密度函数：
分布函数：

【注意】
（1）相互独立的指数分布最小值函数仍服从指数分布
设相互独立， ==>

（2）无记忆性：
例如：

（3）


【例题】假设服从参数为的指数分布，对作 3 次独立重复观察，至少有一次观测值大于 2 的 概率为,则________.

点击展开答案

令事件A为观测值大于2，A发生的次数为Y。
则有：


==>

【例题2】 设随机变量 服从参数 的指数分布，则

点击展开答案



正态分布 ​

正态分布

概率密度 ​

概率密度:

正态分布性质 ​

（1）

（2）

（3）(可加性) 相互独立, 且
则

【注意】独立正态分布的线性组合，期望与原线性组合一致，方差则把减号改成加号，系数平方

（4）标准正态分布 ，，。分布函数

（5）正态分布标准化. 若 , 则

（6）的分布函数为概率密度为

【证明】若，则

新的随机变量：

得证：

【加深理解】，

【例题1】若随机变量 的概率密度是 , 则

点击展开答案

【例题2】若随机变量 的分布函数是 ，则

点击展开答案

【例题3】若随机变量 的分布函数是 ，则

点击展开答案

【例题4】求

点击展开答案

标准正态分布的性质 ​

（1）标准正态分布的概率密度为偶函数

（2）

（3） 或

（4）

（5）若X的概率密度含有 ==> X一定服从一个正态分布 ==> 立刻给二次配方成
==>

（6）若则

二维正态分布 ​

二维正态分布

（1）二维正态分布联合概率密度

（2）若
①

② X, Y独立 <==> <==> X,Y不相关

③ 不需独立

④ 也服从二维正态分布，

⑤ 且X，Y独立 <==>

【例题】
问：X和独不独立

点击展开答案

二维正态分布 独立 <==> <==>


--> ==>

可知：X和独立

【例题2】设随机变量服从二维正态分布 , 则下列随机变量中服从标准正态 分布且与独立的是( )
(A)
(B)
(C)
(D)

点击展开答案

(C)正确，证明如下：




==>
需要满足：

分布中的定理 ​

【定理1】设X为连续型随机变量（连续的） ==> 服从在 ，上的均匀分布

【证明】设
（1）当时，
（2）当时，
（3）当时，

解得： ==>

【例题1】设 服从 上的均匀分布，则 服从分布 ________

点击展开答案


==> ==>

【例题2】设随机变量 的概率密度为 其他， 为 的分布函数， 为 的数学期望，则

点击展开答案

==>

有概率密度，说明X一定是一个连续型随机变量 ==> ==>

【注意】
（1）怎么判断X是连续型随机变量
<==> X有概率密度
<==> F(X)连续

（2）若只取中间一段的表达式，定理依然成立

【例题3】设服从[0,3]上的均匀分布，则服从分布

点击展开答案

服从分布

分布参数的可加性 ​

【总结】参数可加性（独立）

（1） ，则

（2） ，则

（3） ，则

（4） ，则

（5） ，则

分布的期望 ​

分布的方差 ​

连续型随机变量求概率 ​

【注意】连续型随机变量求概率：在哪求概率就在哪求积分

一维随机变量：
二维随机变量：

求一维连续型随机变量的分布函数 ​

总结：已知一维连续型X的概率密度，求的分布

【解题步骤】
第一步：根据X的范围非零的部分求的范围（画的图）
第二步： 时时
第三步：时，
代入
反解范围根据

【要诀】盯着大写（小写字母看成常数，只看大写字母，求的是大写字母的概率，用大写字母的密度）

【例题】设 其他 令 求 .

点击展开答案

第一步：

可知：的图像为
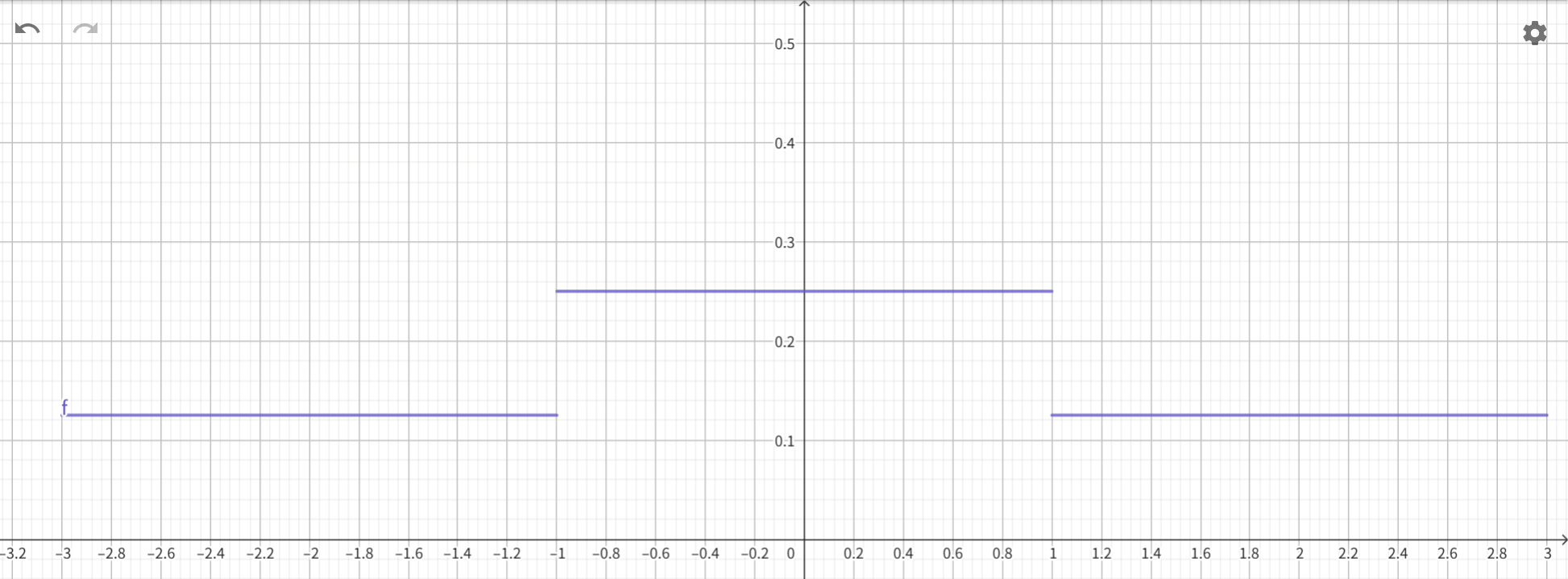
alt text

再画出的图像
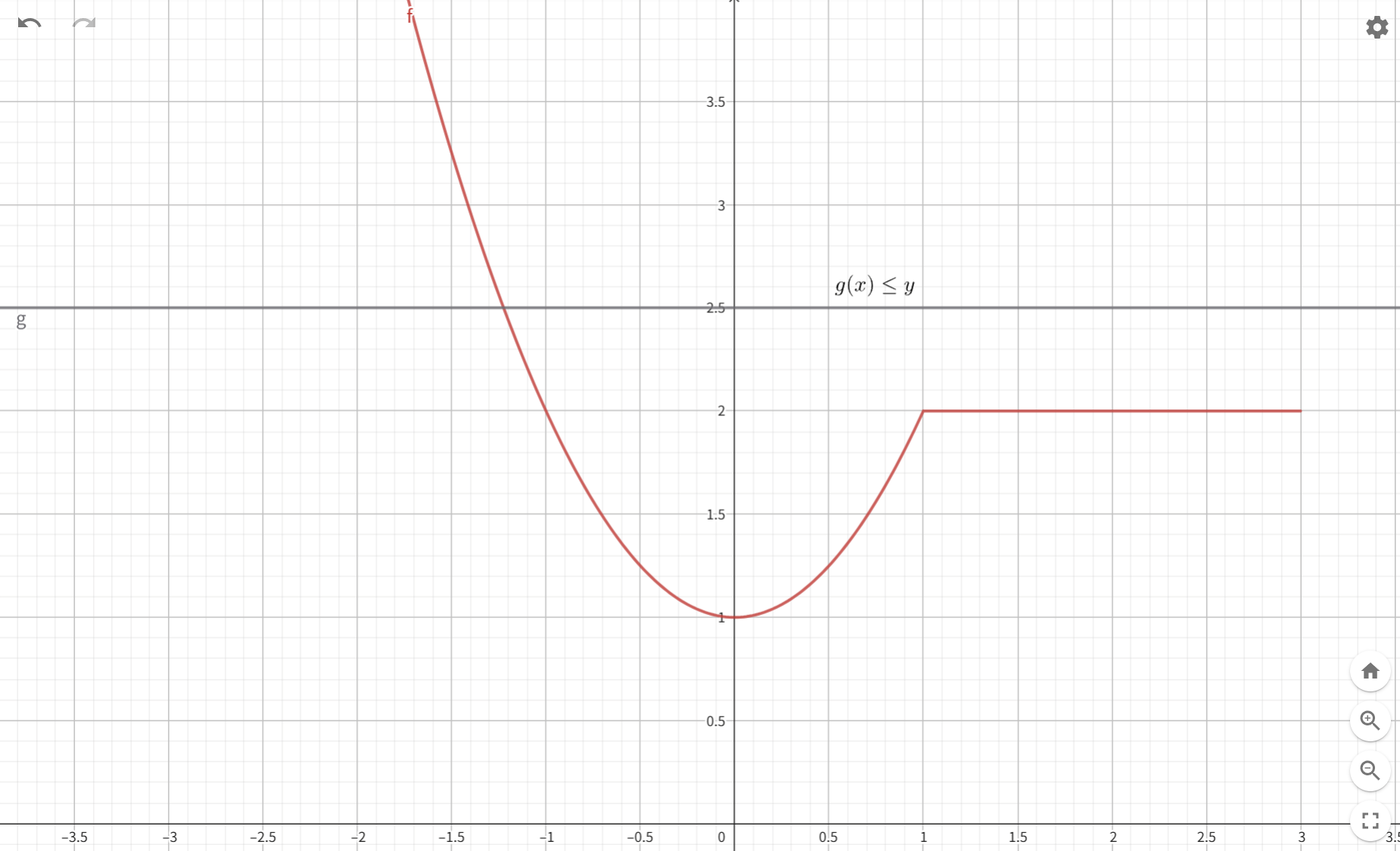
alt text

第二步：
时时

第三步：
时
写出定义：
根据图像可分为两段：
（1）时，

根据的图像可解得：

（2）

根据的图像分三段积分可解得：

综上：

二位连续型随机变量 ​

联合 ​

若在点处连续，有

边缘 ​



条件 ​

二维连续型随机变量的分布 ​

二维随机变量函数的分布（一维）

【五大题型】
（1）都离散
（2）都连续 （）
（3）一离一连，且独立
（4）一离一连，且不独立
（5）其他（最大值最小值的分布）

【题型1】都离散
步骤：
（1）写出所有可能的取值，有重复的合并
（2）计算（所有情况概率相加）
（3）拼成分布律

【例题】已知的联合分布律

（1）求的分布律
（2）求 的分布律

点击展开答案





【题型3】一离一连，且独立

【步骤】
全概率打开根据离散取值
代前面
利用独立

【例题】随机变量X与Y相互独立，且

设，求Z的概率密度

点击展开答案




【总结1】有限个相互独立的随机变量最大最小值的分布
设是相互独立的随机变量，分布函数分别为
则分布函数
分布函数
特别地，若独立同分布，且分布函数均为
则分布函数， 分布函数

【证明】令

是相互独立的随机变量 ==>

令

是相互独立的随机变量
==>
]

【例题1】设随机变量和相互独立，已知的分布函数为,则随机变量的分布函数_______.

二维随机变量独立 ​

二维随机变量独立性

（1）定义：

（2）二维连续型随机变量独立
<==>
<==>

【例题1】独立其他其他

==> 其他

已知当且仅当函数部分可分离范围范围分开不要融合在一起 ==> 独立

（3）若独立，则仍独立

（4）若独立 ==>

（5）二维离散型随机变量独立 <==> 有

（6）服从二维正态分布： 不相关 ==> 独立

（7）证不独立的方法：
各构造一个事件（）
若着两个事件不独立，则不独立（即：）
或相关（） ==> 不独立

古典概型 ​

（1）定义：①有限个样本点 ② 每个样本点等可能

（2）

数字特征 ​

一维随机变量的数学期望 ​

（1）离散（分布律），则
（2）连续（概率密度），则

一维随机变量函数的数学期望 ​

（1）离散（分布律），则
（2）连续（概率密度），则

二维随机变量的数学期望 ​

（1）离散（求分布律），则
（2）连续（联合概率密度），则

运算性质 ​

期望 ​

（1）
（2）
（3）
（4）
（5）
（6）独立不相关

方差 ​

（1）
（2）
（3）
（4）
（5）
（当独立，不相关） ==>
（6） <==>

【注意】求方差（只有一次项）
（1）删掉常数项
（2）求，平方项写,交叉项写

【例题】


协方差 ​

（1）
（2）
（3）
（4）
（5）
（6）
（7）
设独立/不相关，则

【注意】如何化简协方差
（1）删掉常数项
（2）直接算，平方项写,交叉项写

【例题】


相关系数 ​

（1）
（2）若，则不相关
（3）
（4）
（5）， 若 <==>
（6）独立 ==> <==> 不相关
（7） <==> <==> <==>

常见分布的期望方差表 ​

离散型随机变量 ​

离散型随机变量分布律期望方差二项分布泊松分布几何分布

连续型随机变量 ​

连续型随机变量概率密度期望方差均匀分布其他指数分布正态分布

全概率和贝叶斯 ​

全概率公式 ​

设是一个完备事件组（瓜分了全集）
（1）
（2）两两互斥（两两相交为空集）
则


有限可加性
乘法公式

【注意】A的概率等于A带着完备事件组元素一起发生概率的和

【注意】什么时候用全概率公式 ————分类讨论
能找到一个晚辈时间组且A一定带着一个发生

【例题】小明从宿舍去图书馆，他步行，骑自行车，打出租车，坐火车去图书馆的概率分别为0.1,0.2,0.3,0.4,他步行，骑自行车，打出租车，坐火车能到达图书馆的概率分别为0.4,0.3,0.2,0.1
问：
(1) 他能到图书馆的概率
(2) 如果他没到图书馆，他坐火车去的概率

点击展开答案

去图书馆的方式构成完备事件组：
能到图书馆的事件为A


贝叶斯公式（条件概率） ​

设是一个完备事件组（瓜分了全集）

数理统计 ​

（1）统计量的期望和方差
（2）三大分布（）
（3）正态总体的抽样分布（统计量/统计量改一下的分布）

常见统计量 ​

统计量就是一些随机变量的函数

（1）样本均值：
本质：n个随机变量：独立同分布

（2）样本方差：

（3）样本二阶中间矩：

（4）样本二阶原点矩：

【结论1】设独立同分布,且

==>

==> （但若，则）

【证明1】

相互独立

【例题1】设独立同分布,且，则为_______.

点击展开答案


相互独立协方差为

求统计量的抽样分布 ​

卡方分布 ​

【例题】设 为来自总体 的简单随机样本，

当 ，， ， 时，。

点击展开答案

四个平方之和服从，所以四个平方都服从

根据正态分布的性质可得：
==> ==>

==> ==>

【例题】设为来自总体的简单随机样本，记，则下列结论中不正确的是（）

(A) 服从分布。

(B) 服从分布。

(C) 服从分布。

(D) 服从分布。

点击展开答案

不服从卡方分布

统二：

统一：

F分布 ​

(2001,数三)设为来自总体 的简单随机样本，则服从__________分布，参数为____.$

点击展开答案

【例题】 已知 , 样本 取自总体 , 则统计量 服从的分布是

(A) .

(B) .

(C) .

(D) .

点击展开答案

(10)【答案】A.

【解析】由题设知：. 且服从二维正态分布, 又, 从而服从二维正态分布.

又由

,

得, 从而与相互独立.

故与相互独立, 都服从, 因此有

,

.

故应选(A).

t分布 ​

【例题】(2012, 数三)设 为来自总体的简单随机样本，则 的分布为【】

(A)

(B)

(C)

(D)

【例题】设 为来自总体 的简单随机样本. 令 , 则 ( )

(A) .

(B) .

(C) .

(D) .

点击展开答案

解 由于 为样本均值, 故 . 于是, .

根据抽样分布定理(2), 有 .

又因为 与 相互独立, 所以

.

应选 B.

(10)设，，，，是取自总体的简单随机样本，若统计量，则与的值为

(A)，。

(B)，。

(C)，。

(D)，。

点击展开答案

(10)【答案】C.

【解析】由题设，知：。

。

，由分布的典型模式知：

，。

抽样分布综合 ​

【例 6.7】(2005, 数一) 设 为来自总体 的简单随机样本， 与 分别为样本均值与样本方差，则【】

(A)

(B)

(C)

(D)

(9) 设 为来自总体 的简单随机样本, 为来自总体 的简单随机样本, 且两样本相互独立. 记 , , , , 则 ( )

(A) .

(B) .

(C) .

(D) .

22.（本题满分12分）

设随机变量X，Y相互独立，同服从N(0,1).

(1) 问(2X+Y, X-2Y)是否服从二维正态分布? 2X+Y与X-2Y是否相互独立?

(2) 问服从何分布? 并说明理由.

(3) 求.

点击展开答案

22.【解】

由于(X,Y)~N(0,0;1,1;0), 且, 所以(2X+Y, X-2Y)服从二维正态分布. 又因为 , 所以2X+Y与X-2Y不相关, 进而2X+Y与X-2Y相互独立.

统计量的数字特征 ​

【例 6.3】设 为来自总体 的简单随机样本，则

例6.8）(2008, 数一、三) 设 为来自总体 的简单随机样本. 若

(1) 证明 为 的无偏估计量； (2) 当 , 时, 求 .

矩估计 ​

(2002,数三)设总体 的概率密度为

为来自总体的简单随机样本，则未知参数的矩估计量为_

(16)设 是来自对数级数分布

的一个简单随机样本，则 的矩估计量为 ________.

点击展开答案

(16)【答案】

【解析】总体一阶原点矩为

但由很难解出, 所以再求总体的二阶原点矩

由, 两式相除, 得的矩估计量为

最大似然估计 ​

(10)设总体X的概率分布为，，利用来自总体的样本值1,3,2,2,1,3,1,2可得的最大似然估计值为（）.

(A)

(B)

(C)

(D)

点击展开答案

==>

10.设总体X的概率分布为,, 为未知参数， 利用来自总体X的样本值得到经验分布函数，可得的最大似然估计值为().

A.

B.

C.

D.

点击展开答案

10.【答案】A.

【解】由题意，样本的观测值出现了三个1，三个2，二个3， 似然函数， 取对数； 求导，得. 故正确答案为A.

【例 7.2】（2011，数一）设 为来自正态总体 的简单随机样本，其中 已知， 未知，样本均值为 ，样本方差为 .

(I) 求 的最大似然估计量 ;

(II) 求 与 .

点击展开答案

(I)
对样本值，似然函数为

==>

(II)

==>
==>
==>

==>
==>

(23) (本题满分11分) 设随机变量 与 相互独立且分别服从正态分布 与 ，其中 是未知参数且 。记 。 (I) 求 的概率密度 ; (II) 设 为来自总体 的简单随机样本，求 的最大似然估计量 ; (III) 证明 为 的无偏估计量。

点击展开答案

分析 本题主要考查正态分布的概念与性质、最大似然估计法以及无偏估计量的概念。

(1) 服从正态分布 的随机变量 的概率密度为

(2) 若 ， 且 相互独立，则 ,

解 (I) 由于相互独立且服从正态分布的随机变量的线性组合仍服从正态分布, 且

故, 从而 的概率密度

(II) 设是来自于样本的一个样本值, 则似然函数为取对数得令,

即有, 解得.

于是的最大似然估计量为

(III) 由于

故为 的无偏估计量, 结论得证.

(14)设总体X的概率密度为其他其中是未知参数,为来自总体X的简单随机样本,若是的无偏估计,则________

点击展开答案



==>

(23) (本题满分 11 分)

设总体 的概率密度为 其他 其中 为未知参数. , 自该总体的简单随机样本.

(I) 求 的矩估计量;

(II) 求 的最大似然估计量.

点击展开答案

==>

令 ==>

对样本值,似然估计为：

关于单调递增 ==> 的最大似然估计为

[例 7.4]设总体的概率密度为,其中为未知参数，

为来自总体 的简单随机样本.

(I)求的最大似然估计量,

(II)问是否为的 无 偏 估 计 量 ? 并 说 明 理 由 .

点击展开答案

对样本值 , 似然函数为

i取对数求导数
ii (θ出现一次) → 易观察
-->最大似然估计量

假设检验 ​

双侧 ​

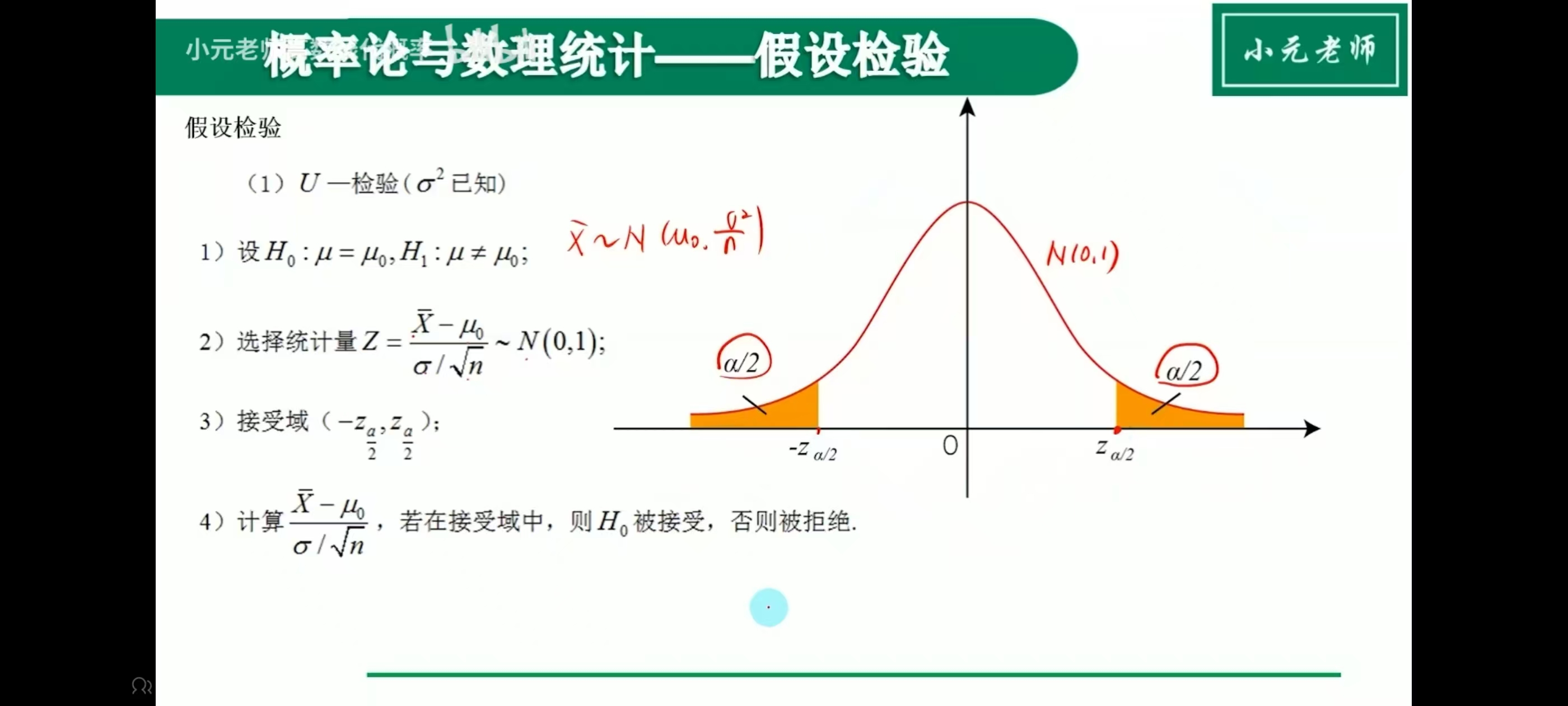
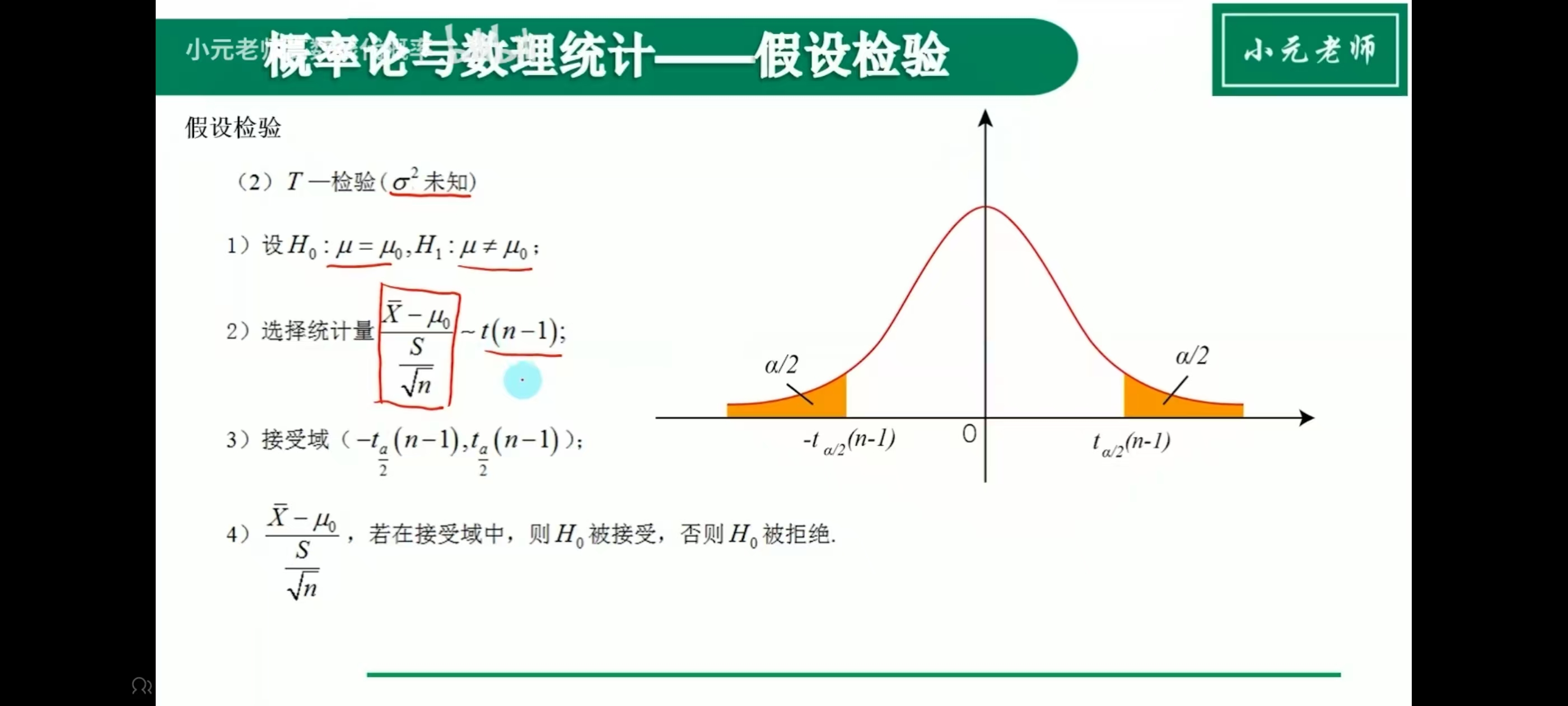
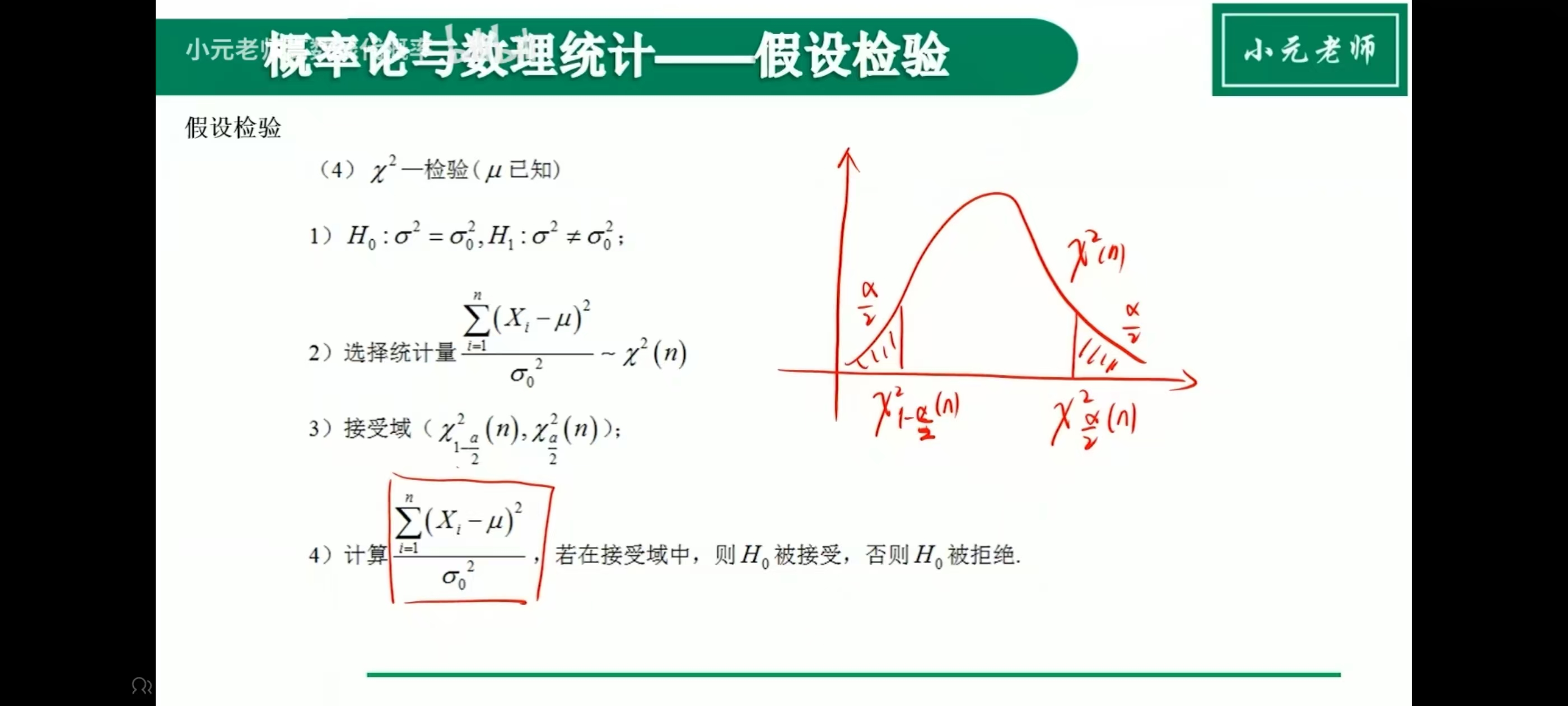
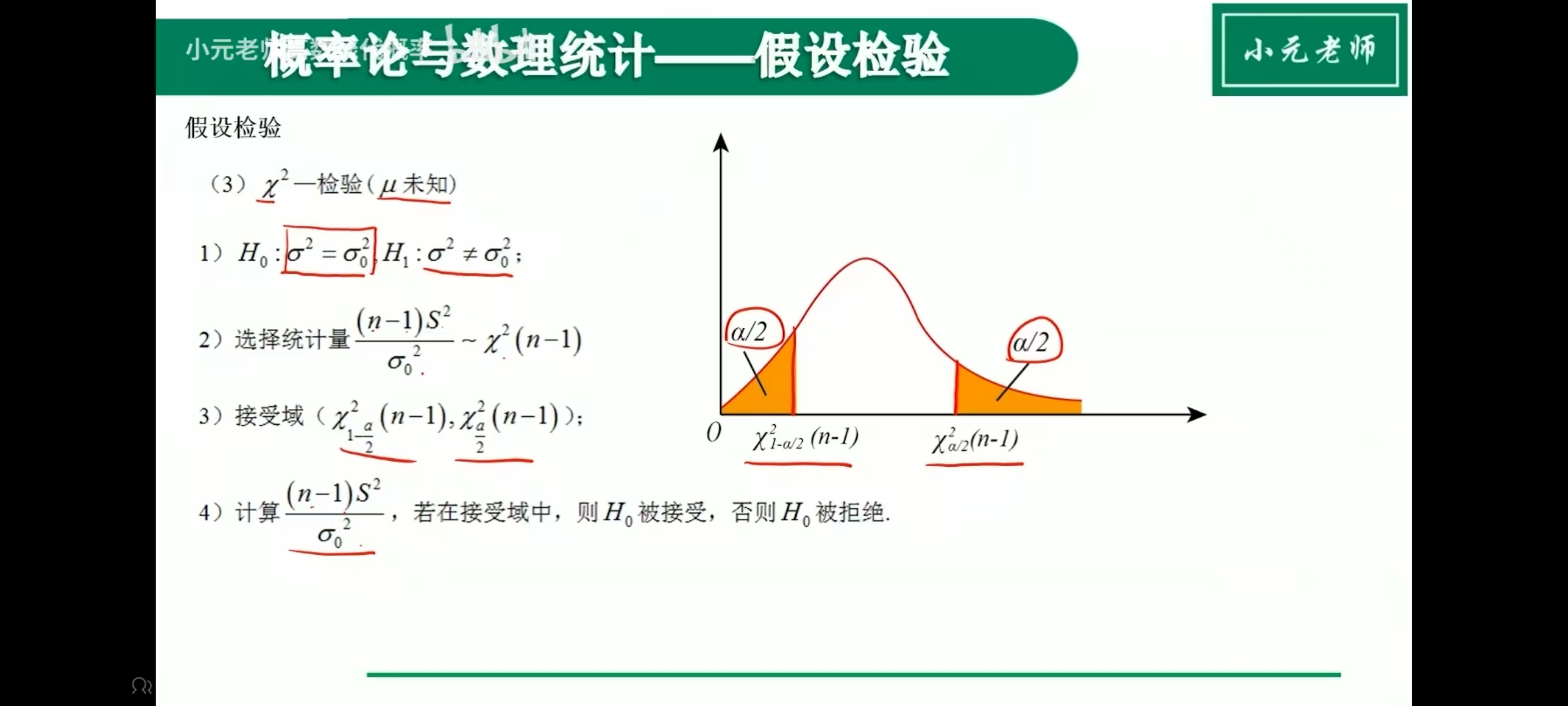
单侧 ​

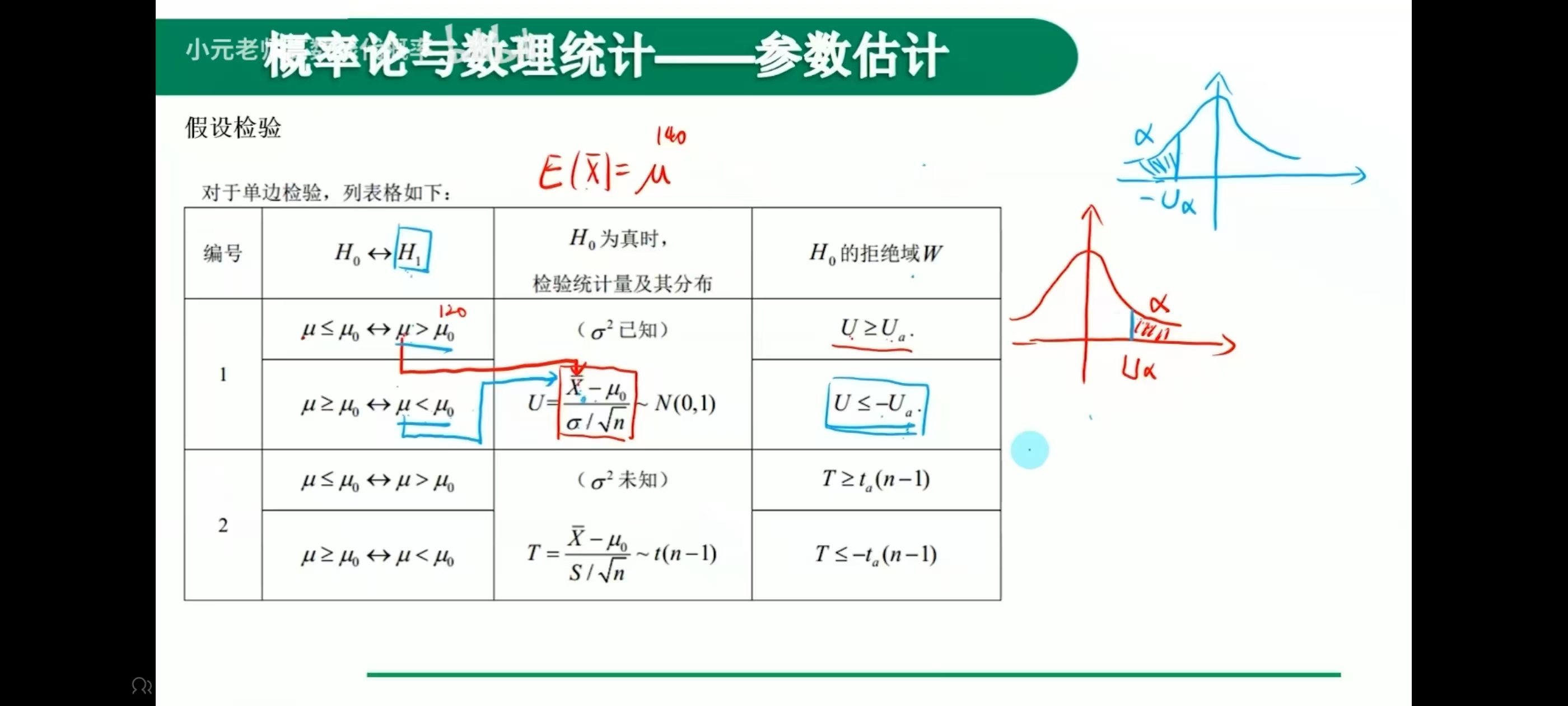
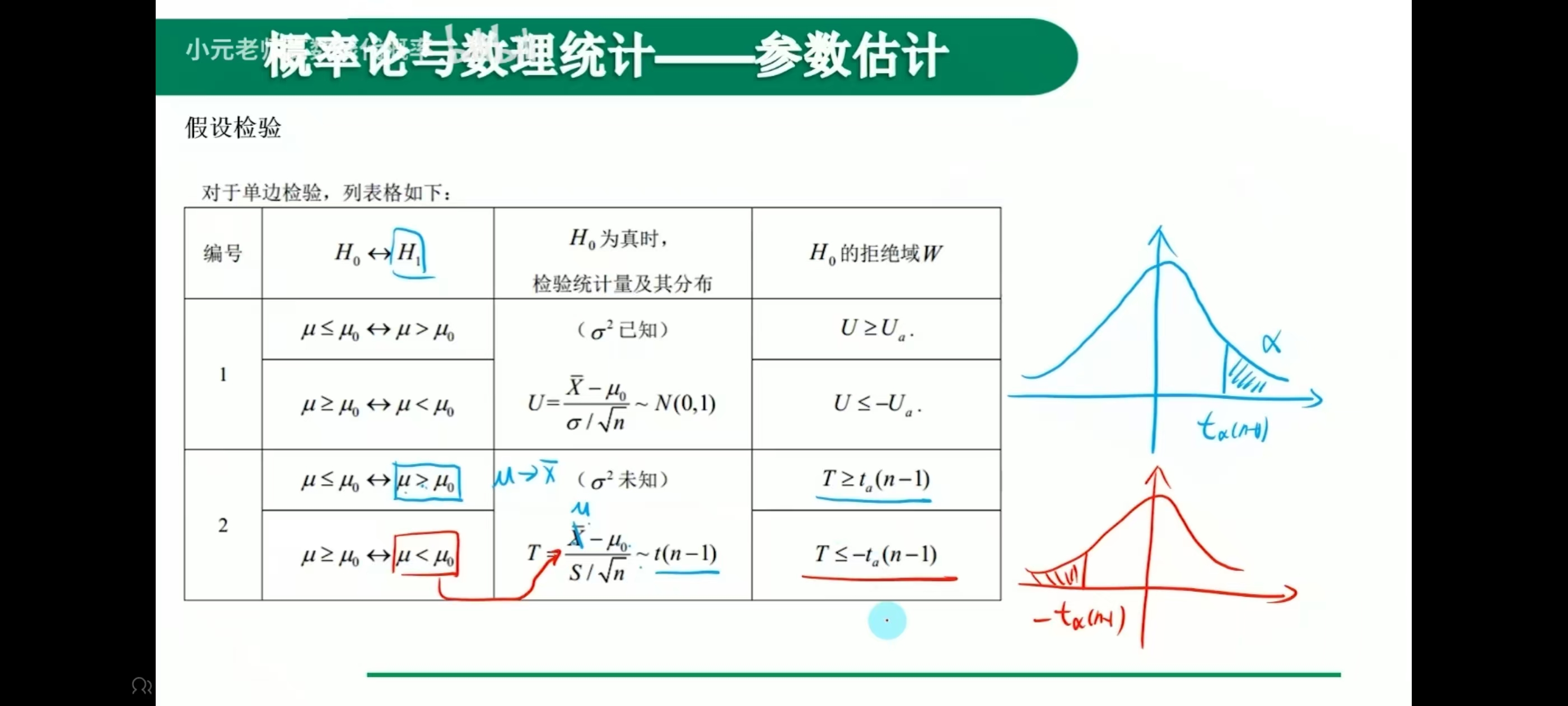
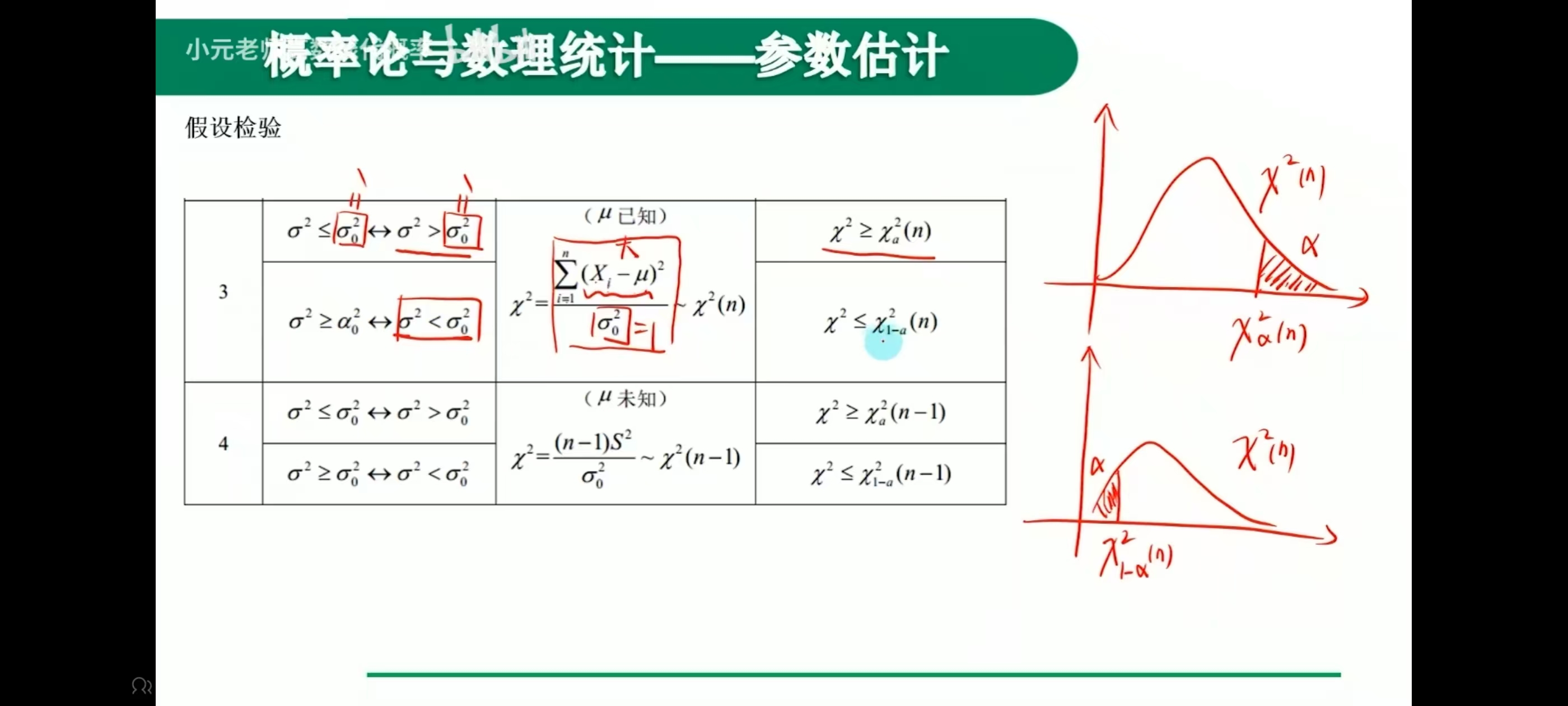
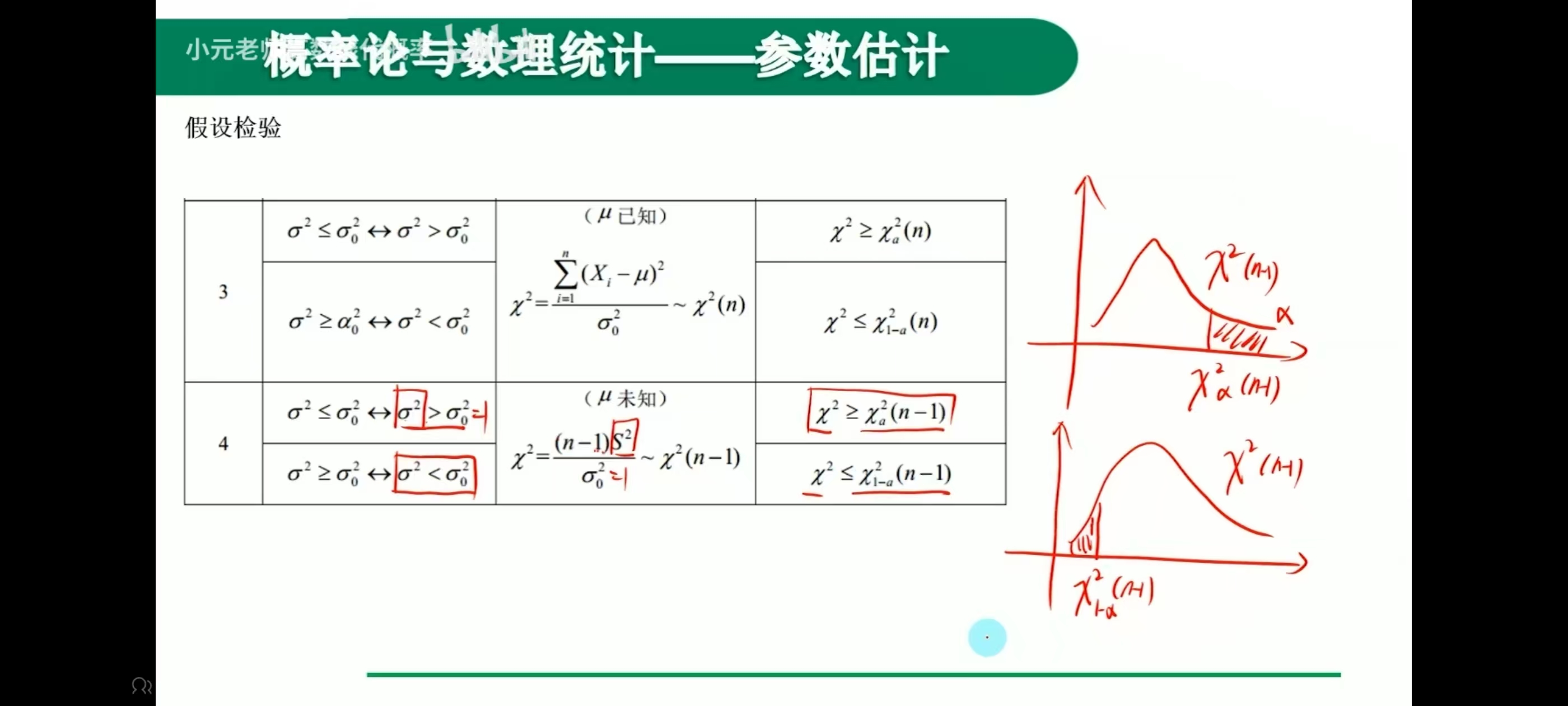
例题 ​

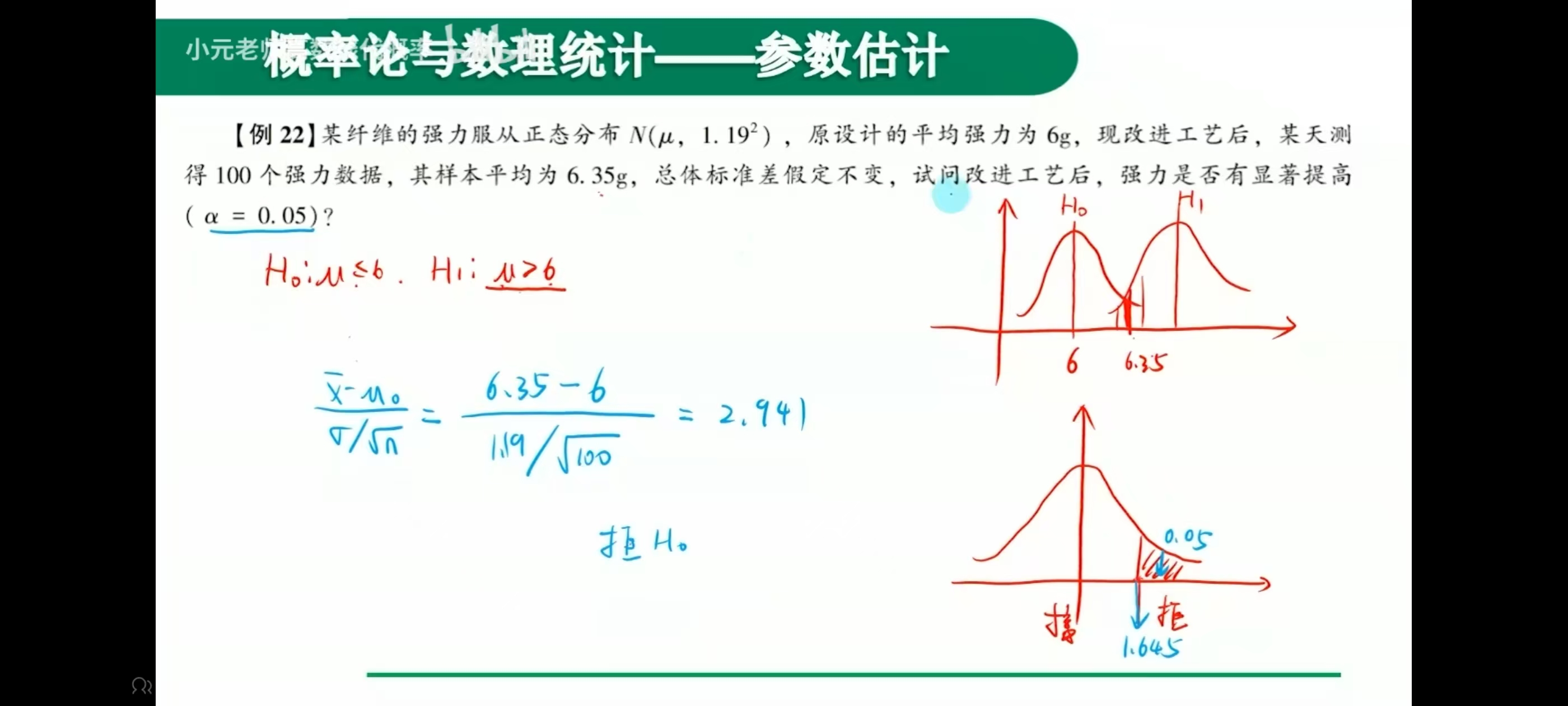
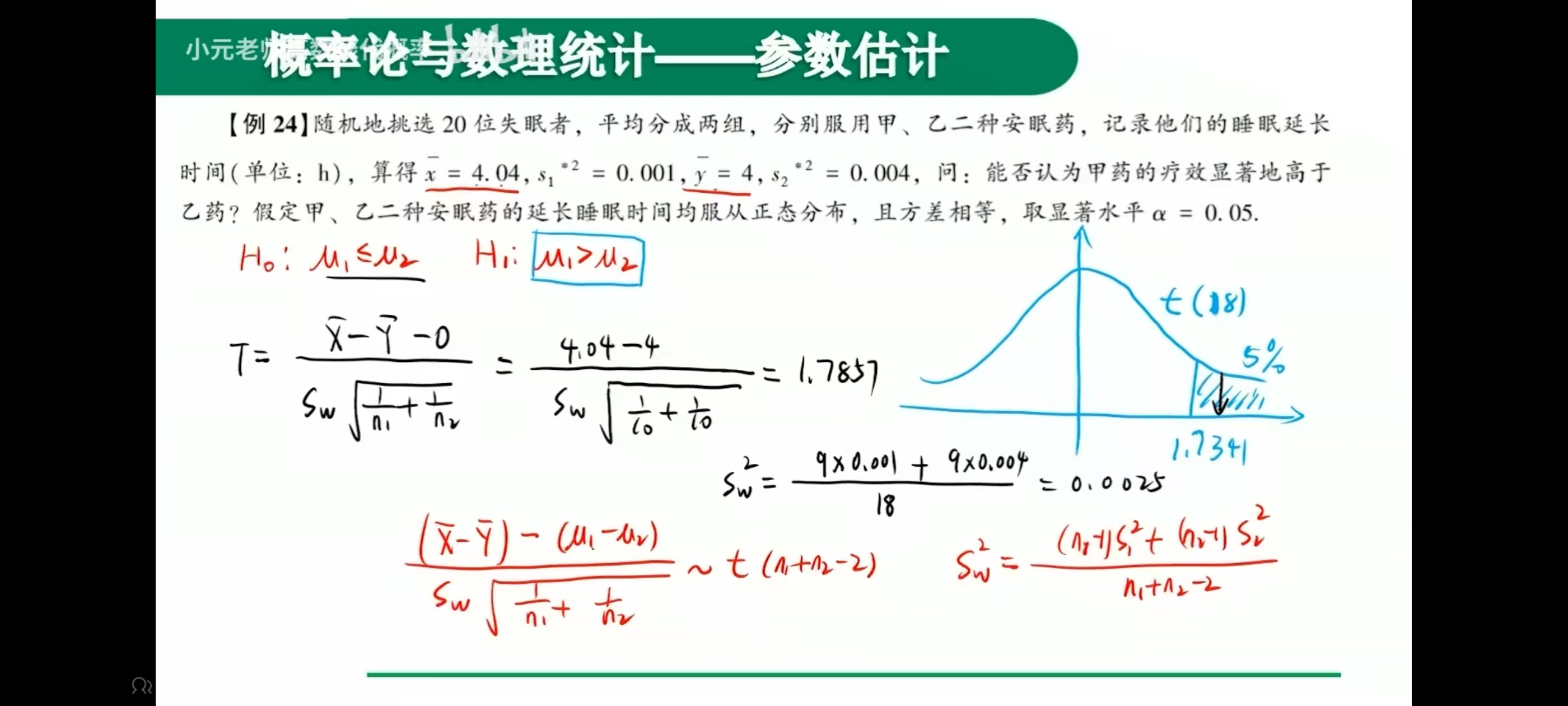
特殊值法 ​

常用特殊函数 ​

（1）
（2）
（3）

（4）

（5）

（6）

说明函数连续性，可导性，导数连续性 （7）

（8）（函数有界，导数无界）

Last updated:

Copyright@ 2024 daidai Shangguan