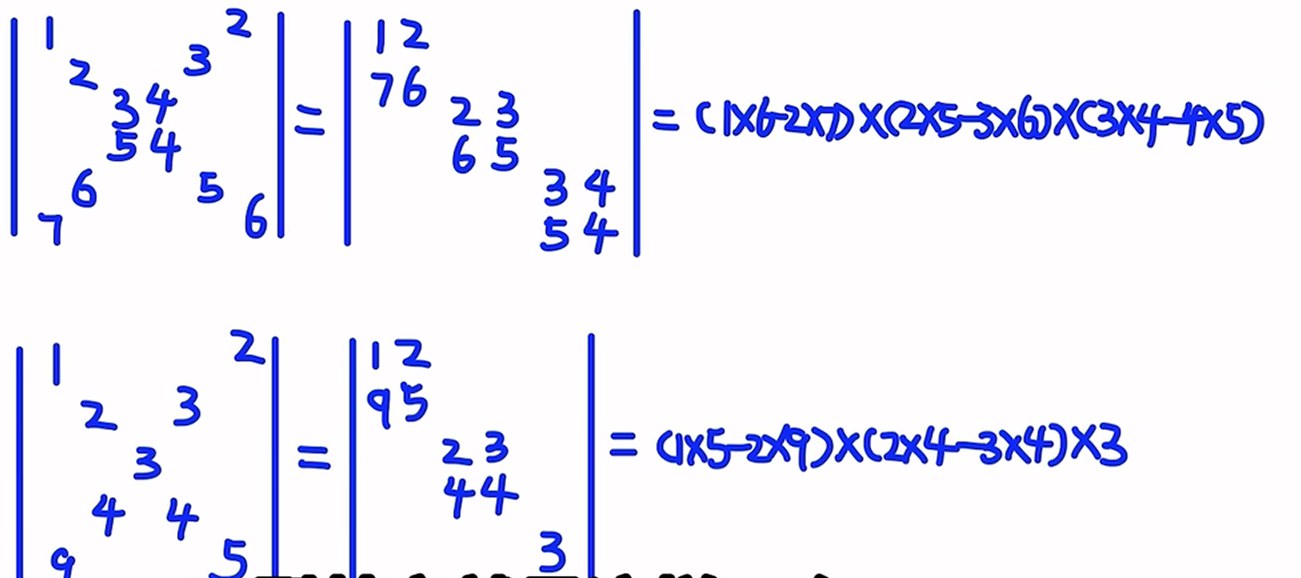线性代数 行列式 行列式的定义 定义:所有取自不同行,不同列元素乘积的代数和D = | a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n | n × n
D = ∑ j 1 j 2 ⋯ j n ( − 1 ) τ ( j , j 2 , ⋯ j n ) a 1 j 1 , a 2 j 2 ⋯ a n j n
注: τ ( j 1 , j 2 , ⋯ j n ) ( j 1 , j 2 , ⋯ j n ) 后 面 有 个 比 他 小 的 数 , 后 面 有 个 比 他 小 的 数 τ ( 54321 ) = 4 + 3 + 2 + 1 + 0 = 10 5 后 面 有 4 个 比 他 小 的 数 , 4 后 面 有 3 个 比 他 小 的 数 ∑ j 1 j 2 ⋯ j n 1 , 2 , ⋯ , n 种 排 列 方 式 ( n ! 种 排 列 方 式 )
代数余子式 总结:行列式a i j A i j
余子式求和 1.余子式求和
2.具体代数余子式求和
3.与各行/列元素之和结合
4.求所有代数余子式之和
三阶行列式的对角线法则 | a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 |
具体行列式的计算 1.做零展开
2.利用行列式的性质化成特殊行列式计算| A T | = | A | | 2 3 4 1 2 3 1 1 1 | = | 1 + 1 2 + 1 3 + 1 1 2 3 1 1 1 | = | 1 2 3 1 2 3 1 1 1 | + | 1 1 1 1 2 3 1 1 1 | = 0 + 0 = 0
(2)特殊行列式| a 11 a 12 a 13 0 a 22 a 23 0 0 a 33 | = | a 11 0 0 a 21 a 22 0 a 31 a 32 a 33 | = a 11 ⋅ a 22 ⋅ a 33
② 副对角线的上(下)三角行列式的值等于它的负对角线元素乘积乘以( − 1 ) n ( n − 1 ) 2 | a 11 a 12 a 13 a 21 a 22 0 a 31 0 0 | = | 0 0 a 13 0 a 22 a 23 a 31 a 32 a 33 | = ( − 1 ) n ( n − 1 ) 2 a 13 a 22 a 31
【记忆】23阶添负号,45阶不变号
③ 范德蒙德行列式第 二 行 中 , 所 有 的 大 下 标 小 下 标 的 乘 积 | 1 1 ⋯ 1 a 1 a 2 ⋯ a n a 1 2 a 2 2 ⋯ a n 2 ⋮ ⋮ ⋱ ⋮ a 1 n − 1 a 2 n − 1 ⋯ a n n − 1 | = 第 二 行 中 , 所 有 的 大 下 标 − 小 下 标 的 乘 积
例:| 1 + x 3 x x 2 x 3 2 1 1 1 0 − 1 1 − 1 9 2 4 8 | = | 1 + x 3 2 0 9 x 1 − 1 2 x 2 1 1 4 x 3 1 − 1 8 | = | 1 1 1 1 x 1 − 1 2 x 2 1 1 4 x 3 1 − 1 8 | = ( 2 − x ) ( 2 − 1 ) ( 2 + 1 ) ( − 1 − x ) ( − 1 − 1 ) ( 1 − x )
3.每行(列)和相等,每列(行)都加到第1列(行),提k做1消0每 行 都 加 到 第 一 行 提 做 | 1 + a 1 1 1 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a | ⇒ 每 行 都 加 到 第 一 行 | 10 + a 10 + a 10 + a 10 + a 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a | ⇒ 提 k 做 1 ( 10 + a ) | 1 1 1 1 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a | = ( 10 + a ) | 1 1 1 1 a a a | = ( 10 + a ) a 3
4.爪形行列式| 1 1 1 1 1 a 1 2 a 1 3 a | = | 1 − 1 a 0 1 1 1 a 1 2 a 1 3 a | = | 1 − 1 a − 1 2 a 0 0 1 1 a 1 2 a 1 3 a | = | 1 − 1 a − 1 2 a − 1 3 a 0 0 0 1 a 1 2 a 1 3 a | = ( 1 − 1 a − 1 2 a − 1 3 a ) 6 a 3
5.利用分块矩阵计算行列式(拉普拉斯)| A 0 0 B | = | A | ⋅ | B |
| 0 A n × n B m × m 0 | = ( − 1 ) m − n | A | | B |
例:D = | 0 a b 0 a 0 0 b 0 c d 0 c 0 0 d | = − | 0 a b 0 0 c d 0 a 0 0 b c 0 0 d | = | a 0 b 0 c 0 d 0 0 a 0 b 0 c 0 d | = − | a b 0 0 c d 0 0 0 0 a b 0 0 c d | = − | a b c a | ⋅ | a b c d | = − ( a d − b c ) 2
6.三线形行列式
D n = | α + β α 0 ⋯ 0 0 β α + β α ⋯ 0 0 0 β α + β ⋯ 0 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ α + β α 0 0 0 ⋯ β α + β | D n = | α + β α β 0 ⋯ 0 0 1 α + β α β ⋯ 0 0 0 1 α + β ⋯ 0 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ α + β α β 0 0 0 ⋯ 1 α + β | 有相同的结论:
D n = { ( n + 1 ) α n , α = β α n + 1 − β n + 1 α − β , α ≠ β . 7.三线形行列式的变形
8.ab形行列式| a b b ⋯ b b a b ⋯ b b b a ⋯ b ⋮ ⋮ ⋮ ⋱ ⋮ b b b ⋯ a | n × n = [ a + ( n − 1 ) b ] ( a − b ) n − 1
证明:每 行 都 加 到 第 一 行 | a b b ⋯ b b a b ⋯ b b b a ⋯ b ⋮ ⋮ ⋮ ⋱ ⋮ b b b ⋯ a | ⇒ 每 行 都 加 到 第 一 行 [ a + ( n − 1 ) b ] | 1 1 1 ⋯ 1 b a b ⋯ b b b a ⋯ b ⋮ ⋮ ⋮ ⋱ ⋮ b b b ⋯ a | = [ a + ( n − 1 ) b ] ( a − b ) n − 1
9.叉形行列式
抽象行列式的计算 行列式的公式:| A T | = | A | | k A | = k n | A | | A B | = | A | ⋅ | B | | A ∗ | = | A | n − 1 | A − 1 | = | A | − 1 = 1 | A | | A | = A B ⇒ | A | = | B | ± 1
行列式重要结论 A为n阶矩阵,如果有k阶子式行列式的值不为0,则说明r ( A ) ≥ k
矩阵 矩阵的运算 该部分摘抄于这篇文章,总结的很好捏 ]
方阵满足乘法交换律的条件 乘法交换律即:( A B = B A )
(1) A f ( A ) , A − 1 , A ∗ f ( A ) , g ( A )
例如:A A ∗ = A ∗ A Λ 1 Λ 2 = Λ 2 Λ 1 A m A t = A t A m ( A + E ) ( A − E ) = ( A − E ) ( A + E )
注:若A与B可交换,则关于AB的运算和数的运算是一样的可 交 换 A , B 可 交 换 ⇒ ( A + B ) 2 = A 2 + 2 A B + B 2 可 交 换 A , B 可 交 换 ⇒ ( A + B ) n = C n 0 A n + C n n − 1 B + ⋯ + C n n B n 可 交 换 A , B 可 交 换 ⇒ A 2 − A − 2 E = ( A + E ) ( A − 2 E )
逆运算 1、( A − 1 ) − 1 = A
2、( A T ) − 1 = ( A − 1 ) T
3、( A m ) − 1 = ( A − 1 ) m
4、( A ∗ ) − 1 = ( A − 1 ) ∗
5、| A − 1 | = | A | − 1
6、( k A ) − 1 = k − 1 A − 1
7、( A B ) − 1 = B − 1 A − 1
8、( A 1 A 2 ⋯ A m ) − 1 = A m − 1 A m − 1 − 1 ⋯ A 1 − 1
转置运算 1、( A T ) T = A
2、( A − 1 ) T = ( A T ) − 1
3、( A m ) T = ( A T ) m
4、( A ∗ ) T = ( A T ) ∗
5、| A T | = | A |
6、( k A ) T = k A T
7、( A B ) T = B T A T
8、( A 1 A 2 ⋯ A m ) T = A m T A m − 1 T ⋯ A 1 T
幂运算 1、( A − 1 ) m = ( A m ) − 1
2、( A T ) m = ( A m ) T
3、( A ∗ ) m = ( A m ) ∗
4、| A | m = | A m |
5、| k A | = k n | A |
6、| A 1 A 2 ⋯ A m | = | A 1 | | A 2 | ⋯ | A m |
伴随运算 1、( A ∗ ) ∗ = | A | n − 2 A
2、重 伴 随 ( ⋯ ( ( ( A ∗ ) ∗ ) ∗ ) ⋯ ) ∗ ( k 重伴随 ) = | A | ( n − 1 ) k − ( − 1 ) k n ⋅ A ( − 1 ) k
3、( A − 1 ) ∗ = ( A ∗ ) − 1
4、( A m ) ∗ = ( A ∗ ) m
5、| A ∗ | = | A | n − 1
6、| k A | ∗ = k n − 1 A ∗
7、( A B ) ∗ = B ∗ A ∗
8、( A 1 A 2 ⋯ A m ) ∗ = A m ∗ A m − 1 ∗ ⋯ A 1 ∗
转置、逆、伴随、k次幂可交换 ( A ∗ ) − 1 = ( A − 1 ) ∗ ( A 4 ) ∗ = ( A ∗ ) 4 ⋯
分块矩阵 分块矩阵的运算 (1)[ A B ] − 1 = [ A − 1 B − 1 ] [ A B ] − 1 = [ B − 1 A − 1 ] [ A B ] n = [ A n B n ] | A 0 ∗ B | = | A | | B | | A ∗ 0 B | = | A | | B | | 0 A m B n ∗ | = ( − 1 ) m n | A | | B | | ∗ A m B n 0 | = ( − 1 ) m n | A | | B |
注:| A B C D | ≠ | A D − B C | [ A B C D ] ∗ ≠ [ D − B − C A ] [ A B ] n ≠ [ A n B n ] ≠ [ A n B n ]
分块矩阵结论 (1)r ( A , B ) ≥ m a x { r ( A ) , r ( B ) }
(2)( A , B ) T = r ( A T B T )
对角矩阵 [ a 1 b 1 a 2 b 2 a 3 b 3 ] = [ a 1 a 2 a 3 ] [ b 1 b 2 b 3 ]
初等矩阵 初等矩阵是指由单位矩阵经过一次初等变换得到的矩阵。
口诀:左行右列
初等矩阵的指令 (1)交换行列
作用在矩阵上的口诀:左行右列
广义初等变换(分块矩阵) 【例 2.7】(2018 数一二三)设 A B为n阶矩阵( X Y )
(A)r ( A A B ) = r ( A )
(B)r ( A B A ) = r ( A )
(C)r ( A B ) = m a x { r ( A ) , r ( B ) }
(D)r ( A B ) = r ( A T B T )
(A)r ( A 0 ) = r ( A )
(B)
(C)r ( A B ) ≥ m a x { r ( A ) , r ( B ) }
(D)r ( A B ) = ( A T B T )
代数余子式 A = [ a 11 a 12 a 21 a 22 ]
余子式: M 11 = a 22 , M 12 = a 21 , M 21 = a 12 , M 22 = a 11
代数余子式:A n m = ( − 1 ) n + m M n m
【例2.9】(2023,数一)设n阶矩阵A,B,C满足ABC=O,记矩阵( O A B C E ) ( A B C O E ) ( E A B A B O )
设A B C n r ( A C O B ) = r ( A ) + r ( B ) C A
(A) 必要非充分条件
(B) 充分非必要条件
(C) 充分必要条件
(D) 既非充分又非必要条件
【详解】必要性:若C A n P C = A P
列 变 换 ( A C O B ) → 列变换 ( A O O B ) r ( A C O B ) = r ( A ) + r ( B )
充分性:令A = ( 1 0 0 0 ) B = ( 0 0 0 1 ) C = ( 0 0 0 1 ) r ( A C O B ) = r ( A ) + r ( B ) C A
矩阵乘法 向量角度计算矩阵乘法
伴随矩阵 定义:A = [ a 11 a 12 a 21 a 22 ] ⇒ A ∗ = [ A 11 A 12 A 21 A 22 ] T = [ A 11 A 21 A 12 A 22 ]
性质:A A ∗ = A ∗ A = | A | E A A ∗ ( A ∗ ) − 1 = | A | E A ( A ∗ ) − 1 A = | A | ( A ∗ ) − 1 A − 1 = 1 | A | A ∗ | A ∗ | = | A | n − 1
伴随矩阵的秩 r ( A ∗ ) { n r ( A ) = n 1 r ( A ) = n − 1 0 r ( A ) < n − 1
二阶矩阵的伴随 二阶矩阵的伴随:A = [ a b c d ] ⇒ A ∗ = [ d − b − c a ]
例题:矩阵A A ∗ = [ 4 − 2 0 0 − 3 1 0 0 0 0 − 4 0 0 0 0 − 1 ] A = _ _ _ _ _ _ .
令B = [ 4 − 2 − 3 1 ] C = [ − 4 0 0 − 1 ] A ∗ = [ B 0 0 C ]
| A ∗ | = | A | n − 1 = | A | 3 = | B | | C | = − 8 ⇒ | A | = − 2 ( A ∗ ) − 1 = [ B C ] − 1 = [ B − 1 C − 1 ]
B − 1 = 1 | B | B ∗ = 1 − 2 [ 1 2 3 4 ] C − 1 = 1 | C | C ∗ = 1 4 [ − 1 − 4 ]
A = | A | ( A ∗ ) − 1 = − 2 [ B − 1 C − 1 ]
元素之和 各行元素之和:A ⋅ ( 1 1 ⋮ 1 ) = ( Σ A 1 i Σ A 2 i ⋮ Σ A n i )
各列元素之和:A T ⋅ ( 1 1 ⋮ 1 ) = ( Σ A 1 i Σ A 2 i ⋮ Σ A n i )
逆矩阵 可逆的定义 定义:若n阶方阵A , B { A B = E B A = E 可 逆 , 且 可 逆 , 且 { A 可 逆 , 且 A − 1 = B B 可 逆 , 且 B − 1 = A
结论1:n阶方阵A , B A B = E B A = E A B = E ⇒ B A = E B A = A − 1 A B A = E B A = E
结论2:若n阶方阵A , B A B = E B A = E 可 逆 , 且 可 逆 , 且 { A 可 逆 , 且 A − 1 = B B 可 逆 , 且 B − 1 = A
可逆六充要 n A
⟺ | A | ≠ 0
⟺ r ( A ) = n
⟺ A
⟺ A x = 0
⟺ A x = b
⟺ A
【口诀】秩满可逆不为0 无关唯一只零解
常规求逆 [ A | E ] ⇒ [ E | A − 1 ]
二阶矩阵的逆 常用伴随矩阵计算:A − 1 = 1 | A | A ∗ 参考这个口诀快速计算
三阶矩阵求逆 【机械三阶求逆法】
由该例题讲解过程:A = [ 1 2 − 1 − 1 − 2 2 1 3 0 ]
第一步:先将前两列往第三列后面抄
[ 1 2 − 1 1 2 − 1 − 2 2 − 1 − 2 1 3 0 1 3 ]
第二步:再将前两行往第三行后面抄
[ 1 2 − 1 1 2 − 1 − 2 2 − 1 − 2 1 3 0 1 3 1 2 − 1 1 2 − 1 − 2 2 − 1 − 2 ]
第三步:划掉第一行和第一列
[ − 2 2 − 1 − 2 3 0 1 3 2 − 1 1 2 − 2 2 − 1 − 2 ]
第四步:竖算横抄得伴随(算:如第一个数为− 2 × 0 − 2 × 3 = − 6
A ∗ = [ − 6 − 3 2 2 1 − 1 − 1 − 1 0 ]
第五步:伴随转逆
A − 1 = A ∗ | A |
初等矩阵的逆 初等矩阵均可逆,且它的逆矩阵是同类型的初等矩阵1 k − k
对角矩阵的逆 ( a 1 a 2 ⋱ a 2 ) − 1 = ( 1 a 1 1 a 2 ⋱ 1 a n ) ; ( a 1 a 2 . . a n ) − 1 = ( 1 a n 1 a n − 1 . . 1 a 1 ) .
分块矩阵的逆 前提:、 可 逆 A 、 D 可 逆
[ A 0 0 D ] − 1 = [ A − 1 0 0 D − 1 ] ,
[ 0 A D 0 ] − 1 = [ 0 D − 1 A − 1 0 ] ,
[ A 0 C D ] − 1 = [ A − 1 0 − D − 1 C A − 1 D − 1 ] ,
[ A B 0 D ] − 1 = [ A − 1 − A − 1 B D − 1 0 D − 1 ] .
对称矩阵与反对称矩阵定义 设 A n A T = A A A T = − A A
【评注】任意 n
A = 1 2 ( A + A T ) + 1 2 ( A − A T ) 为 对 称 ( A + A T ) T = A T + ( A T ) T = A T + A = A T + A T ( A + A T 为 对 称 ) 为 反 对 称 ( A − A T ) T = A T − ( A T ) T = A T − A = − ( A − A T ) ( A − A T 为 反 对 称 )
解矩阵方程 解矩阵方程A X = B ⇒ X = ?
取逆 (1)求行 变 换 A − 1 B [ A ∣ B ] ⇒ 行 变 换 [ E ∣ A − 1 B ] 列 变 换 A B − 1 [ B A ] ⇒ 列 变 换 [ E A B − 1 ]
由(1)可得,A X = B ⇒ X = A − 1 B X B = A ⇒ X = A B − 1
【例4.12】(2014, 数一、二、三)设A = ( 1 − 2 3 − 4 0 1 − 1 1 1 2 0 − 3 )
(I) 求线性方程组A x = 0
(II) 求满足A B = E B
( A ∣ E ) = ( 1 − 2 3 − 4 1 0 0 0 1 − 1 1 0 1 0 1 2 0 − 3 0 0 1 ) → ( 1 0 0 1 2 6 − 1 0 1 0 − 2 − 1 − 3 1 0 0 1 − 3 − 1 − 4 1 )
(I)ξ = ( − 1 2 3 1 )
(II)X = [ 2 − k 1 6 − k 2 − 1 − k 3 − 1 + 2 k 1 − 3 + 2 k 2 1 + 2 k 3 − 1 + 3 k 1 − 4 + 3 k 2 1 + 3 k 3 k 1 k 2 k 3 ]
已知a A = ( 1 2 a 1 3 0 2 7 − a ) = ( 1 a 2 0 1 1 − 1 1 1 ) .
(I)求a ;
(II)求满足AP = B P .
解 (Ⅰ) 由于矩阵A可经初等列变换化为矩阵B, 故矩阵方程AX=B有解. 于是, r(A)=r(A,B). 对(A,B)作初等行变换.
( A , B ) = ( 1 2 a 1 a 2 1 3 0 0 1 1 2 7 − a − 1 1 1 ) r 2 − r 1 r 3 − 2 r 1 ( 1 2 a 1 a 2 0 1 − a − 1 1 − a − 1 0 3 − 3 a − 3 1 − 2 a − 3 ) r 1 − 2 r 2 r 3 ∗ − 3 r 2 ∗ ( 1 0 3 a 3 3 a − 2 4 0 1 − a − 1 1 − a − 1 0 0 0 0 a − 2 0 ) . 当且仅当a=2时, r(A)=r(A,B)=2. 或者, 由矩阵A可经初等列变换化为矩阵B可知, A的列秩等于B的列秩, 从而r(A)=r(B). 同上面的计算可知r(A)=2, 当且仅当a=2时, r(A)=r(B). 因此, a=2.
待定系数法 令X = [ x 1 x 2 x 3 x 4 ]
分块矩阵法(重要) A X = B ⇒ X = ? / X A = B ⇒ X = ? X , B A ( ξ 1 , ξ 2 , ξ 3 ) = ( β 1 , β 2 , β 3 ) A X = β 1 ⇒ X = ξ 1 A X = β 2 ⇒ X = ξ 2 A X = β 3 ⇒ X = ξ 3 ξ 1 , ξ 2 , ξ 3 X
矩阵的n次方 找规律 方法:求一下A 2 , A 3 ,
例:已知 A = [ 1 0 1 0 2 0 1 0 1 ] A n
A 2 = [ 1 0 1 0 2 0 1 0 1 ] ⋅ [ 1 0 1 0 2 0 1 0 1 ] = [ 2 0 2 0 4 0 2 0 2 ] = 2 A ⋯ A n = 2 n − 1 A
列乘行矩阵(秩为1) 列乘行是一个矩阵,行乘列是一个数
列乘行矩阵特征:A = α β T [ 2 − 1 3 4 − 2 6 − 2 1 − 3 ]
列乘行矩阵性质:A n = t r n − 1 ( A ) ⋅ A
注:A = α β T A = α β T t r ( A ) = α T β = β T α A = [ 1 2 3 ] [ 1 , 2 , 3 ] t r ( A ) = 1 2 + 2 2 + 3 2 = 14 A = α β T A 2 = A ⋅ A = α β T α β T = t r ( A ) α β T = t r ( A ) ⋅ A A 3 = A ⋅ A ⋅ A = α β T ⋅ α β T ⋅ α β T = t r 2 ( A ) A ⋯ A n = t r n − 1 ( A ) ⋅ A
特殊的幂0矩阵 幂0矩阵的定义:存在某个幂次,再次之后全为0
矩阵对角线元素全为0,对角线一侧也全为0[ 0 a d f 0 0 b e 0 0 0 c 0 0 0 0 ] [ 0 0 0 0 a 0 0 0 d b 0 0 f e c 0 ]
求A 2 , A 3 , A 4 A 2 = [ 0 0 a b a e + c d 0 0 0 b c 0 0 0 0 0 0 0 0 ] A 3 = [ 0 0 0 a b b c 0 0 0 0 0 0 0 0 0 0 0 0 ] A 4 = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ]
二项式定理 A n = ( k E + B ) n , B
二项式定理:( A + B ) n = C n 0 A n B 0 + C n 1 A n − 1 B 1 + C n r A n − r B r + ⋯ + C n n A 0 B n
注:A 0 = E
例:A = [ 2 1 1 0 2 3 0 0 2 ] A n A = [ 2 0 0 0 2 0 0 0 2 ] + [ 0 1 1 0 0 3 0 0 0 ] = 2 E + [ 0 1 1 0 0 3 0 0 0 ]
令 令 B = [ 0 1 1 0 0 3 0 0 0 ] , A = ( 2 E + B ) B 2 = [ 0 0 3 0 0 0 0 0 0 ] B 3 = 0
A n = ( 2 E + B ) n = C n 0 B 0 ( 2 E ) n + C n 1 B 1 ( 2 E ) n − 1 + C n 2 B 2 ( 2 E ) n − 2 = 2 n E + n ⋅ B ⋅ 2 n − 1 ⋅ E + n ( n − 1 ) 2 B 2 ⋅ 2 n − 2 ⋅ E = [ 2 n 2 n 2 n ] + 2 n − 1 ⋅ n [ 0 1 1 0 0 3 0 0 0 ] + 2 n − 3 ⋅ n ( n − 1 ) [ 0 0 3 0 0 0 0 0 0 ]
分块矩阵的n次方 A = [ B 0 0 C ] , A n = [ B n 0 0 C n ]
相似对角化 方法:A Λ P − 1 A P = Λ A = P Λ p − 1 A n = P Λ n P − 1
(1)[ λ 1 λ 2 λ 3 ⋱ λ n ] n = [ λ 1 n λ 2 n λ 3 n ⋱ λ n n ] A P = P Λ A P = P B A P = P Λ A = P Λ P − 1 A n = P Λ n P − 1
例题:设 P A = B P P = [ 0 2 4 1 0 0 0 3 5 ] B = [ 1 0 0 0 − 1 0 0 0 − 1 ] A 100 = _ _ _ _ _ _
P − 1 P A = P − 1 B P ⇒ A 100 = P − 1 B 100 P = P − 1 ⋅ [ 1 0 0 0 1 0 0 0 1 ] ⋅ P = P − 1 P = E
行阶梯和行最简 (1)行阶梯形矩阵
(2)行最简形矩阵
矩阵的秩 秩的定义 (1)A有r阶子式不为0r + 1
另一种描述:
求矩阵A的秩 (1)行 变 换 A ⇒ 行 变 换
求含参矩阵A的秩 (1)行 变 换 A ⇒ 行 变 换
矩阵的秩结论 秩不变口诀 【注意区分】左行右列是初等矩阵相乘,是讨论具体矩阵乘积。
左列右行用来讨论矩阵乘积后的秩。
乘可逆矩阵,秩不变
消除律 【消除律】可 逆 或 列 满 秩 A B = A C ⇒ A 可 逆 或 列 满 秩 B = C 可 逆 或 行 满 秩 B A = C A ⇒ A 可 逆 或 行 满 秩 B = C
结论证明:A m × n B n × s = A m × n C n × s r ( A ) = n B = C 左 乘 A B = A C ⇒ 左 乘 A T A T A B = A T A C A T A 可 逆 r ( A T A ) = r ( A ) = n ⇒ A T A 可 逆 B = C
(2)B m × n A n × s = C m × n A n × s r ( A ) = n B = C 右 乘 B A = C A ⇒ 右 乘 A T B A A T = C A A T A A T 可 逆 r ( A A T ) = r ( A ) = n ⇒ A A T 可 逆 B = C
【列/行满秩】n m A r ( A ) = m r ( A ) = n
四秩相等口诀 r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A )
AB=0 证明:如果A B = 0 B A X = 0 r ( A ) = r A X = 0 n − r r ( B ) ≤ n − r = n − r ( A ) r ( A ) + r ( B ) ≤ n n
西尔维斯特不等式 A : m × n , B : n × s r ( A ) + r ( B ) − n ≤ r ( A B ) ≤ m i n { r ( A ) , r ( B ) }
【例题】设 A n × m B m × n C n m ≠ n r ( A ) + r ( B ) + r ( C ) = r ( A B C ) + m + n r ( A B C ) + n = r ( A B ) + r ( C ) r ( A B C ) + m = r ( A B ) + r ( C ) r ( A B ) + n = r ( A ) + r ( B ) r ( A B ) + m = r ( A ) + r ( B )
r ( A ) + r ( B ) + r ( C ) = r ( A B C ) + m + n ≥ r ( A B ) + r ( C ) − n + m + n ≥ r ( A B ) + r ( C ) + m ≥ r ( A ) + r ( B ) − m + m + r ( C ) ≥ r ( A ) + r ( B ) + r ( C )
说明上述不等式,实则均相等
r ( A ) + r ( B ) + r ( C ) = r ( A B C ) + m + n = r ( A B ) + r ( C ) + m
==> r ( A B C ) + n = r ( A B ) + r ( C ) r ( A B ) + m = r ( A ) + r ( B )
矩阵等价 矩阵A与B等价的充要条件 <==> A可经过有限次的初等变换化为B(可行列混用)为 初 等 阵 P s ⋯ P 2 P 1 A Q 1 Q 2 ⋯ Q ρ = B ( P i , Q i 为 初 等 阵 ) 可 逆 P A Q = B ( P , Q 可 逆 ) 为 同 型 阵 , 即 同 为 矩 阵 r ( A ) = r ( B ) ( A , B 为 同 型 阵 , 即 同 为 n × m 矩 阵 )
矩阵A与B行等价的充要条件 <==> A可经过有限次的初等行变换化为B为 初 等 阵 P s ⋯ P 2 P 1 A = B ( P i 为 初 等 阵 ) 可 逆 P A = B ( P 可 逆 )
矩阵A与B列等价的充要条件 <==> A可经过有限次的初等列变换化为B为 初 等 阵 A Q 1 Q 2 ⋯ Q ρ = B ( Q i 为 初 等 阵 ) 可 逆 A Q = B ( Q 可 逆 )
矩阵相似 矩阵相似的性质 (1) 只有方阵,才谈相似
(2)(定义)对于n阶方阵A , B ∈ P s . t . P − 1 A P = B A ∼ B
(3)若A ∼ B f ( A ) ∼ f ( B ) A − 1 ∼ B − 1 A ∗ ∼ B ∗ A T ∼ B T f ( A ) + k A − 1 + ρ A ∗ ∼ f ( B ) + k B − 1 + ρ B ∗
A − 1 , A ∗ , f ( A ) A ∼ B P P − 1 A P = B P − 1 A − 1 P = B − 1 P − 1 A ∗ P = B ∗ P − 1 f ( A ) P = f ( B )
==> ( P − 1 A P ) 2 = B 2 ⇒ P − 1 A 2 P = B 2
==> ( P T ) − 1 A T P T = B T | A | = | B | | λ E − A | = | λ E − B | r ( A ) = r ( B ) t r ( A ) = t r ( B )
(4)若A可逆,则A B ∼ B A
证明:看 成 整 体 A − 1 A B A = B A ⇒ A B 看 成 整 体 A B ∼ B A
(5)若A ∼ B , C ∼ D [ A 0 0 C ] ∼ [ B 0 0 D ]
(6)实对称矩阵和非对称矩阵一定不相似
(7)可相似对角化的矩阵和不能相似对角化的矩阵一定不相似
【注意】A ∼ B P − 1 A P = B
{ P 1 − 1 A P 1 = Λ P 2 − 1 B P 2 = Λ ⇒ P 1 − 1 A P 1 = P 2 − 1 B P 2
左 乘 右 乘 ⇒ 左 乘 P 2 右 乘 P 2 − 1 P 2 P 1 − 1 A P 1 P 2 − 1 = B ⇒ ( P 1 P 2 − 1 ) − 1 A ( P 1 P 2 − 1 ) = B
令P = P 1 P 2 − 1 ⇒ P − 1 A P = B
列 变 换 [ P 2 P 1 ] ⇒ 列 变 换 [ E P 1 P 2 − 1 ] = P
【注意】A ∼ B P − 1 A P = B
(待定系数法)P = ( α 1 , α 2 , α 3 ) A P = P B α 1 , α 2 , α 3
A = [ 1 0 0 0 0 0 0 1 0 ] B = [ 0 0 1 0 1 0 0 0 0 ]
的 特 征 值 有 ⇒ A 的 特 征 值 有 : 0 , 0 , 1 的 特 征 向 量 有 ⇒ A 的 特 征 向 量 有 : α 1 = [ 0 0 1 ] α 2 = [ 1 0 0 ] ⇒ { A α 1 = 0 A α 2 = α 2
令P = ( α 1 , α 2 , α 3 ) A P = P B ⇒ A ( α 1 , α 2 , α 3 ) = ( α 1 , α 2 , α 3 ) [ 0 0 1 0 1 0 0 0 0 ] ⇒ ( A α 1 , A α 2 , A α 3 ) = ( 0 , α 2 , α 1 ) ⇒ ( 0 , α 2 , A α 3 ) = ( 0 , α 2 , α 1 ) ⇒ A α 3 = [ 0 0 1 ] α 3 A X = [ 0 0 1 ]
A X = [ 0 0 1 ] [ 0 1 k ]
解得:P = ( α 1 , α 2 , α 3 ) = [ 0 1 0 0 0 1 1 0 k ]
判断A与B是否相似 (1)用性质排除
(2)均 可 相 似 对 角 化 与 特 征 值 一 样 才 相 似 一 个 可 相 似 对 角 化 一 个 不 可 相 似 对 角 化 一 定 不 相 似 均 不 可 相 似 对 角 化 才 相 似 只 适 用 于 三 阶 以 下 { A , B 均 可 相 似 对 角 化 , A 与 B 特 征 值 一 样 才 相 似 A , B 一 个 可 相 似 对 角 化 , 一 个 不 可 相 似 对 角 化 , 一 定 不 相 似 A , B 均 不 可 相 似 对 角 化 , r ( A − λ E ) = r ( B − λ E ) 才 相 似 ( 只 适 用 于 三 阶 以 下 )
【例题】( 1 1 0 0 1 1 0 0 1 )
(A) ( 1 1 − 1 0 1 1 0 0 1 ) ( B ) ( 1 0 − 1 0 1 1 0 0 1 ) ( C ) ( 1 1 − 1 0 1 0 0 0 1 ) ( D ) ( 1 0 − 1 0 1 0 0 0 1 )
题干和选项的特征值均为三重k特征值,且均r ( A − E ) ≠ 0
三阶不可相似对角化矩阵可考虑第三种判断方法:r ( A − E ) = 2 r ( A − E ) = 2
矩阵相似对角阵结论 A ∼ Λ P − 1 A P = Λ Λ λ
证明:P − 1 A P = Λ A P = P Λ P = ( α 1 , α 2 , α 3 ) A ( α 1 , α 2 , α 3 ) = ( α 1 , α 2 , α 3 ) [ λ 1 λ 2 λ 3 ] ( A α 1 , A α 2 , A α 3 ) = ( λ 1 α 1 , λ 2 α 2 , λ 3 α 3 ) { A α 1 = λ 1 α 1 A α 2 = λ 2 α 2 A α 3 = λ 3 α 3
矩阵可相似对角化条件 (1)充要条件λ λ 重 数 r ( A − λ E ) = n − 重 数
证明:k重特征值λ , ( A − λ E ) X = 0 n − r ( A − λ E ) = k r ( A − λ E ) = n − k
(2)充分条件f ( A ) = 0 f ( A ) f ( A ) = ( A + k 1 E ) ( A + k 2 E ) ⋯ ( A + k i E ) k 1 ≠ k 2 ≠ ⋅ ≠ k i
(3)必要条件r ( A ) = A
注:一般r ( A ) ≥
常用结论:( A K = 0 )
② 若A的特征值只有k(n重),A可相似对角化 <==> A = kE
③ 秩为1矩阵可相似对角化 <==> t r ( A ) ≠ 0
6.设三阶矩阵A ₁ ₂ ₃ λ ₁ = λ ₂ = − 1 , λ ₃ = 2 r ( A + E ) + r ( A − E ) + r ( A − 2 E )
A. 3
6.【答案】D A r ( A + E ) = 2 r ( A − 2 E ) = 2 r ( A − E ) = 3 r ( A + E ) + r ( A − E ) + r ( A − 2 E ) = 7
6.下列矩阵中不能相似于对角矩阵的是
A. ( 1 1 a 0 2 2 0 0 3 ) . B. ( 1 1 a 1 2 0 a 0 3 ) . C. ( 1 1 a 0 2 0 0 0 2 ) . D. ( 1 1 a 0 2 2 0 0 2 ) .
(2017,数一、二、三)设A = ( 2 0 0 0 2 1 0 0 1 ) , B = ( 2 1 0 0 2 0 0 0 1 ) , C = ( 1 0 0 0 2 0 0 0 2 )
(A)A C B C
(C)A C B C
(B)A C B C
(D)A C B C
(5)下列矩阵中,与矩阵( 1 1 0 0 1 1 0 0 1 )
(A)( 1 1 − 1 0 1 1 0 0 1 ) . ( 1 0 − 1 0 1 1 0 0 1 ) . ( 1 1 − 1 0 1 0 0 0 1 ) . ( 1 0 − 1 0 1 0 0 0 1 ) .
矩阵A和A伴随秩的关系 (1)r ( A ∗ ) n , 1 , 0 r ( A ∗ ) = { n r ( A ) = n 1 r ( A ) = n − 1 0 r ( A ) < n − 1
矩阵的特征值和特征向量 两条特征值重要结论 (1)特征值乘积 = 行列式值
(2)特征值之和 = 迹
(3)如果主对角线上的元素,所在行或所在列的其他元素值为0,则该值为矩阵的一个特征值
求解矩阵的特征值 或 | A − λ E | = 0 或 | λ E − A | = 0 ⇒ λ
注:利用| A − λ E | = 0
秩一矩阵的特征值 (1)秩为1的矩阵,特征值为t r ( A ) , 0 , 0 , ⋯ , 0
注:A = α β T 两 向 量 内 积 t r ( A ) = α T β = β T α = 两 向 量 内 积
回看秩一矩阵解矩阵n次方
上三角矩阵的特征值 上三角矩阵的特征值为对角线元素
特征值重要结论 可 逆 A k A A k f ( A ) A − 1 A ∗ P − 1 A P A T λ k λ λ k f ( λ ) 1 λ | A | λ λ λ α α α α α α P − 1 α ⇐ ( k ≠ 0 ) ⇐ ⇐ ( A 可 逆 )
特征向量的定义 A α = λ α
抽象矩阵求特征值和特征向量 (1)A + λ E | A + λ E | = 0 − λ | A + λ E | = 0 − λ ( A + λ E ) X = 0 | A + λ E | = 0 − λ
(2)A的各行元素之和为a,则A有一个特征值a,对应特征向量k ( 1 , 1 , ⋯ , 1 ) T , k ≠ 0
(3)η 1 , η 2 , ⋯ , η n A X = 0 { A η 1 = 0 A η 2 = 0 ⋮ A η s = 0 { A η 1 = 0 ⋅ η 1 A η 2 = 0 ⋅ η 2 ⋮ A η s = 0 ⋅ η s λ 1 = λ 2 = ⋯ = λ s = 0 不 全 为 k 1 η 1 + k 2 η 2 + ⋯ + k s η s ( k 1 ⋯ k s 不 全 为 0 )
(4)若A B = k B A ( β 1 , β 2 , ⋯ , β n ) = k ( β 1 , β 2 , ⋯ , β n )
(5)| A | = 0 且 A B = 0 且 B ≠ 0
(6)f ( A ) = 0 f ( λ ) = 0 λ f ( λ = 0 ) f ( λ ) = 0 λ
(7)特征值重数 ≥
实对称矩阵 定义:A = A T
实对称矩阵的性质 (1)不同特征值对应特征向量正交正 交 矩 阵 ∈ 正 交 矩 阵 Q , s . t . Q − 1 A Q = Q T A Q = Λ A T , A ∗ , A − 1 m × n C C C T , C T C
实对称矩阵的结论 有3阶实对称矩阵A,特征值为λ 1 ≠ λ 2 ≠ λ 3 λ 1 α 1 α 1 λ 2 , λ 3
答:不一定。
例如:3阶实对称矩阵A,特征值为λ 1 = 1 , λ 2 = 2 , λ 3 = 3
有3阶实对称矩阵A,特征值为λ 1 ≠ λ 2 = λ 3 λ 1 α 1 α 1 λ 2 , λ 3
答:一定。
总结:若只剩下一个特征值(不管几重),求特征向量,与其他特征向量正交的向量,一定全是这个特征值的特征向量。
定理1:n阶实对称矩阵A的特征值重 λ 1 , λ 2 ( n − 1 重 ) α 1 λ 1 α α 1 α λ 2
定理2:3阶实对称矩阵A的特征值λ 1 ≠ λ 2 ≠ λ 3 α 1 , α 2 λ 1 , λ 2 α α 1 , α 2 α λ 3
注:求与α 1 , α 2 α = α 1 × α 2
定理3:3阶实对称矩阵A的特征值二 重 λ 1 , λ 2 ( 二 重 ) α 1 , α 2 λ 1 , λ 2 α α 1 , α 2 α λ 2
设矩阵 A = [ 0 − 1 4 − 1 3 a 4 a 0 ] Q Q T A Q Q 1 6 ( 1 , 2 , 1 ) T α , Q
正交矩阵 正交矩阵定义:满足A T A = E A A T = E A
正交矩阵的性质A | A | = 1 A A − 1 , A T A − 1 = A T A , B A ⟺ A A ⟨ A x , A y ⟩ = ⟨ x , y ⟩ ∥ A x ∥ = ∥ x ∥ A A ( 0 − 1 1 0 )
性质七:关于| A + E | | A − E | A | A | < 0 A | A | < 0 A | A | > 0 A A A
A | A | = − 1 ⟶ A i j = − a i j A 是 非 零 矩 阵 | A | = − 1 ← A 是非零矩阵 A i j = − a i j A | A | = 1 ⟶ A i j = a i j A 是 非 零 矩 阵 | A | = 1 ← A 是非零矩阵 A i j = a i j
A ∗ = [ A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋮ A 1 n A 2 n ⋯ A n n ] = [ − a 11 − a 21 ⋯ − a n 1 − a 12 − a 22 ⋯ − a n 2 ⋮ ⋮ ⋮ − a 1 n − a 2 n ⋯ − a n n ] = − [ a 11 a 21 ⋯ a n 1 a 12 a 22 ⋯ a n 2 ⋮ ⋮ ⋮ a 1 n a 2 n ⋯ a n n ] = − A T 二次型 二次型的定义 含有 n 个变量 x_{1}, x_{2}, ⋯, x_{n} 的二次齐次函数 (每一项都是二次)
f ( x 1 , x 2 , ⋯ , x n ) = a 11 x 1 2 + a 22 x 2 2 + ⋯ + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + ⋯ + 2 a 1 n x 1 x n + ⋯ + 2 a n − 1 , n x n − 1 x n 称为 n 元二次型,记作 f = x T A x , x = ( x 1 , x 2 , ⋯ , x n ) T , A = ( a i j ) r ( f )
【评注】二次型与实对称矩阵一一对应,二次型的矩阵 A 的主对角线元素为平方项的系数,其余元素 a j i = a i j x i j
可逆线性变换定义 可逆线性变换的定义 关系式
{ x 1 = c 11 y 1 + c 12 y 2 + ⋯ + c 1 n y n x 2 = c 21 y 1 + c 22 y 2 + ⋯ + c 2 n y n ⋯ ⋯ ⋯ x n = c n 1 y 1 + c n 2 y 2 + ⋯ + c n n y n 即 x = C y
x = ( x 1 x 2 ⋮ x n ) , y = ( y 1 y 2 ⋮ y n ) , C = ( c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋮ ⋮ ⋱ ⋮ c n 1 c n 2 ⋯ c n n ) 称为由变量 x 1 , x 2 , ⋯ , x n y 1 , y 2 , ⋯ , y n C x = C y
标准型 标准型是指只含有平方项的二次型f = d 1 y 1 2 + d 2 y 2 2 + ⋯ + d n y n 2 = y T Λ y
标准型结论 (1)二次型经正交变换为标准形,其特征值不变(常用结论)
求标准形 例题:f = x 1 2 + x 3 2 − 2 x 1 x 2 − 2 x 2 x 3
拉格朗日配方法 (以三元二次型为例)
(1) 若二次型含有平方项, 不妨设含有 x 1 2 x 1 x 2 f = d 1 y 1 2 + d 2 y 2 2 + ⋯ + d n y n 2 x = C y
【总结】第一个括号把x 1 x 2 x 3
(2) 若二次型不含平方项, 不妨设含有 x 1 x 2 { x 1 = y 1 + y 2 x 2 = y 1 − y 2 x 3 = y 3
f = x 1 2 + x 3 2 − 2 x 1 x 2 − 2 x 2 x 3 = ( x 1 2 − 2 x 1 x 2 ) + x 3 2 − 2 x 2 x 3 = ( x 1 2 − 2 x 2 x 1 ) + x 3 2 − 2 x 2 x 3 = ( x 1 − x 0 ) 2 − ( x 2 2 + 2 x 3 x 2 ) + x 3 2 = ( x 1 − x 0 ) 2 − ( x 2 2 + 2 x 3 x 2 + x 3 2 ) + 2 x 3 2 = ( x 1 − x 2 ) 2 − ( x 2 + x 3 ) 2 + 2 x 3 2
令{ x 1 − x 2 = y 1 x 2 + x 3 = y 2 x 3 = y 3
标准形:f = y 1 2 − y 2 2 + 2 y 3 2 f = z 1 2 − z 2 2 + z 3 2
正交变换法三大步 (1) 求二次型的矩阵 A n λ 1 , ⋯ , λ n
(2) 求 A n α 1 , ⋯ , α n
(3) 将不同特征值的特征向量分别 Schmidt 正交化, 得 γ 1 , ⋯ , γ n Q = ( γ 1 , ⋯ , γ n )
经过正交变换 x = Q y f = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2
A = [ 1 − 1 0 − 1 0 − 1 0 − 1 1 ]
| λ E − A | = | λ − 1 1 0 1 λ 1 0 1 λ − 1 | = | λ − 1 1 0 1 λ 1 − ( λ − 1 ) 0 λ − 1 | = | λ − 1 1 0 2 λ 1 0 0 λ − 1 | = ( λ − 1 ) | λ − 1 1 2 λ | = ( λ − 1 ) ( λ − 2 ) ( λ + 1 ) = 0
标准形:f = y 1 2 − y 2 2 + 2 y 3 2 f = z 1 2 − z 2 2 + z 3 2
合同变换法求标准形 合同变换其实就是行列合作共同进行初等变换第 一 列 的 负 一 倍 加 到 第 二 列 第 一 行 的 负 一 倍 加 到 第 二 行 [ 1 2 3 4 5 6 7 8 9 ] ⇒ 第 一 列 的 负 一 倍 加 到 第 二 列 [ 1 1 3 4 1 6 7 1 9 ] ⇒ 第 一 行 的 负 一 倍 加 到 第 二 行 [ 1 1 3 4 1 6 7 1 9 ]
使用合同变换将A化简成对角阵Λ 带 着 做 相 同 的 行 变 换 初 等 列 变 换 [ A E ] ⇒ 带 着 做 相 同 的 行 变 换 初 等 列 变 换 [ Λ C ]
原理:[ A E ] ⇒ r c [ P 1 T A P 1 E P 1 ] ⇒ ⋯ r ⋯ ⋯ c ⋯ [ P n T ⋯ P 1 T A P 1 ⋯ P n P 1 P 2 ⋯ P n ]
令C = P 1 P 2 ⋯ P n P n T ⋯ P 1 T A P 1 ⋯ P n = C T A C P n T ⋯ P 1 T A P 1 ⋯ P n = Λ C T A C = Λ
[ A E ] = [ 1 − 1 0 − 1 0 − 1 0 − 1 1 1 1 1 ] ⇒ [ 1 0 0 − 1 − 1 − 1 0 − 1 1 1 1 0 0 1 0 0 0 1 ] [ 1 0 0 0 − 1 − 1 0 − 1 1 1 1 0 0 1 0 0 0 1 ] ⇒ ⋯ [ 1 0 0 0 − 1 0 0 0 2 1 1 − 1 0 1 − 1 0 0 1 ]
规范形 规范形的定义 若标准形的系数为1,-1或 0,即 f = y 1 2 + y 2 2 + ⋯ + y p 2 − y p + 1 2 − ⋯ − y p + q 2
标准形的正的改成1,负的改成-1,0还是0
正定 正定的定义 设二次型f ( X ) = X T A X ∀ x ≠ 0 f ( X ) = X T A X > 0 f
注:若f f = 0 x = 0 x =≠ 0 , f = 0 f = 2 x 1 2 + x 2 2 + 3 x 3 2 ≥ 0
正定的充要条件 <==> 恒 有 ∀ x ≠ 0 , 恒 有 f = X T A X > 0 f = X T A X
正定的必要条件 ==> A是实对称矩阵| A | > 0
正定的常用结论 (1)A正定 ==> A − 1 , A ∗ f ( A ) = a m A m + a m − 1 A m − 1 + ⋯ + a 0 E a i ≥ 0
总结:已知具体二次型正定,问参数的范围
惯性 惯性指数 惯性指数:f = d 1 y 1 2 + d 2 y 2 2 + ⋯ + d n y n 2
惯性定理 惯性定理:
【注意】可逆线性变换可以理解为可逆换元:X = C Y
【例题】a x 1 2 + ( 2 a − 1 ) x 2 2 + a x 3 2 − 2 x 1 x 2 + 2 a x 1 x 3 − 2 x 2 x 3 p = 1 a ∈ ( 1 , + ∞ ) ( − 1 2 , 1 ) [ − 1 2 , 1 ] ( − ∞ , − 1 2 )
二次型矩阵:A = [ a − 1 a − 1 2 a − 1 − 1 a − 1 a ] | A − λ E | = | a − λ − 1 a − 1 2 a − 1 − λ − 1 a − 1 a − λ | = 0 { λ 1 = 0 λ 2 = 2 a − 2 λ 3 = 2 a + 1
正惯性指数为1,有一个大于0,另外两个小于等于0⇒ { 2 a + 1 > 0 2 a − 2 ≤ 0 ⇒ a ∈ ( − 1 2 , 1 ]
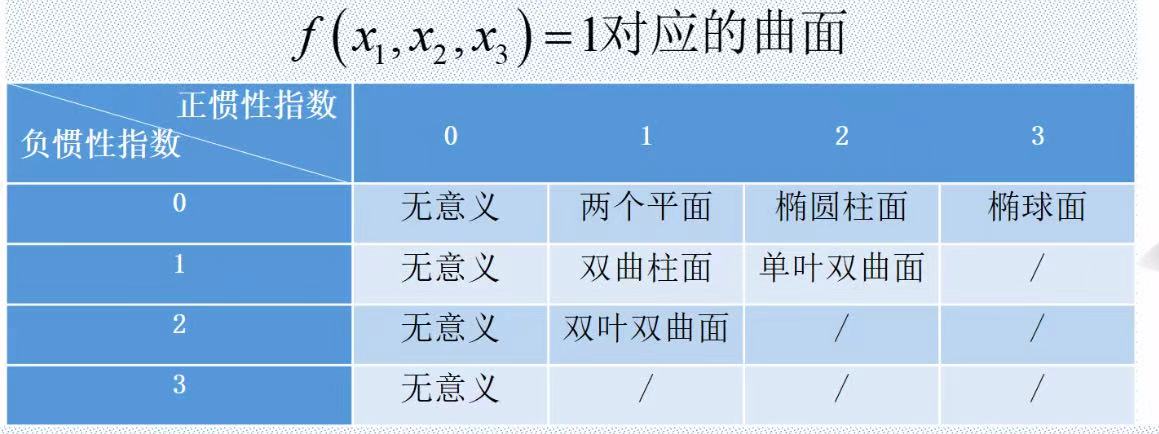
二次型与曲面关系
合同 合同的来源(可逆线性变换) X T A X ⇒ X = C Y ( C Y ) T A ( C Y ) = y T C T A C Y = Y T B Y C T A C = B
什么叫合同变换 【类比】A与B等价 <==> A可经有限次初等变换到B
回顾
合同总结 (1)实对称矩阵A与B合同的条件可 逆 阵 使 得 ∃ 可 逆 阵 C , 使 得 C T A C = B X T A X X T B X r ( A ) = r ( B ) A T B T A − 1 B − 1 A + A T B + B T
实对称矩阵A与B相似 ==> A与B合同
(2)A与B等价,相似,合同的关系与 都 是 实 对 称 矩 阵 ⇒ A 与 B 都 是 实 对 称 矩 阵
注:对称矩阵和非对称阵一定不合同 (也一定相似)
向量组 向量组的思维定势 (1)k α ( k α 1 , k α 2 , k α 3 ) = k ( α 1 , α 2 , α 3 ) a 1 α 1 + a 2 α 2 , b 1 α 1 + b 2 α 2 ( a 1 α 1 + a 2 α 2 , b 1 α 1 + b 2 α 2 ) = ( α 1 , α 2 ) ⋅ [ a 1 b 1 a 2 b 2 ]
向量组线性相关(无关) 定义:k 1 , k 2 , ⋯ , k m k 1 α 1 + k 2 α 2 + ⋯ + k m α m = 0 k 1 , k 2 , ⋯ , k m α 1 , α 2 , ⋯ , α m k 1 , k 2 , ⋯ , k m α 1 , α 2 , ⋯ , α m
(2)向量组α 1 , α 2 , ⋯ , α m
(3)向量组α 1 , α 2 , ⋯ , α m
(4)一个向量构成的向量组线性相关 <==> 它是零向量
(5)两个向量构成的向量组线性相关 <==> 坐标成比例
(6)α 1 , α 2 , ⋯ , α m r ( α 1 , α 2 , ⋯ , α m ) < m α 1 , α 2 , ⋯ , α m r ( α 1 , α 2 , ⋯ , α m ) = m
(7)n个n维向量| α 1 , α 2 , ⋯ , α n | = 0 | α 1 , α 2 , ⋯ , α n | ≠ 0
(8)n+1个n维向量必相关(个数 > 维数,必相关)
向量组线性无关定理 n个线性无关的n维向量可以表示任何一个n维向量
向量组线性表示的等价命题 (1)向量β α 1 , α 2 , ⋯ , α n r ( α 1 , α 2 , ⋯ , α n ) = r ( α 1 , α 2 , ⋯ , α n , β ) = n
(2)向量β α 1 , α 2 , ⋯ , α n r ( α 1 , α 2 , ⋯ , α n ) = r ( α 1 , α 2 , ⋯ , α n , β ) < n
(3)非零向量 β α 1 , α 2 , ⋯ , α s ⇔ ( α 1 , α 2 , ⋯ , α s ) ( x 1 x 2 ⋮ x s ) = β ⇔ r ( α 1 , α 2 , ⋯ , α s ) = r ( α 1 , α 2 , ⋯ , α s | β )
(4)向量β α 1 , α 2 , ⋯ , α n r ( α 1 , α 2 , ⋯ , α n ) ≠ r ( α 1 , α 2 , ⋯ , α n , β ) r ( α 1 , α 2 , ⋯ , α n ) + 1 = r ( α 1 , α 2 , ⋯ , α n , β )
(5)α 1 , α 2 , ⋯ , α s β α 1 , α 2 , ⋯ , α s α 1 , α 2 , ⋯ , α s , β r ( α 1 , α 2 , ⋯ , α s , β ) = r ( α 1 , ⋯ , α s ) + 1 = s + 1
(6)向量组α 1 , α 2 , ⋯ , α m β 1 , β 2 , ⋯ , β s r ( α 1 , α 2 , ⋯ , α m ) = r ( α 1 , α 2 , ⋯ , α m , β 1 , β 2 , ⋯ , β s ) r ( α 1 , α 2 , ⋯ , α m ) ≥ r ( β 1 , β 2 , ⋯ , β s )
口诀:我能表示逆,我比你厉害,我的秩大于等于你的秩
向量组α 1 , α 2 , ⋯ , α m β 1 , β 2 , ⋯ , β s r ( α 1 , α 2 , ⋯ , α m ) < r ( α 1 , α 2 , ⋯ , α m , β 1 , β 2 , ⋯ , β s )
(7)
(8)
(9)向量组α 1 , α 2 , ⋯ , α s α 1 , α 2 , ⋯ , α s , β β α 1 , α 2 , ⋯ , α s r ( α 1 , α 2 , ⋯ , α s ) = s r ( α 1 , α 2 , ⋯ , α s , β ) < s + 1 s = r ( α 1 , α 2 , ⋯ , α s ) ≤ r ( α 1 , α 2 , ⋯ , α s , β ) ≤ s
(10)n个线性无关的n维向量可以表示任何一个n维向量
(11)向量组β 1 , β 2 , ⋯ , β s α 1 , α 2 , ⋯ , α t s > t β 1 , β 2 , ⋯ , β s
(12)向量组α 1 , α 2 , ⋯ , α t β 1 , β 2 , ⋯ , β s β 1 , β 2 , ⋯ , β s t ≥ s
(II)若α 1 = ( 1 , 2 , 1 ) T , α 2 = ( 2 , 5 , 3 ) T , β 1 = ( 2 , 3 , − 1 ) T , β 2 = ( − 1 , 0 , 3 ) T α 1 , α 2 β 1 , β 2
α 1 × α 2 = | i j k 1 2 1 2 5 3 | = i − j + k , β 1 × β 2 = | i j k 2 3 − 1 − 1 0 3 | = 9 i − 5 j + 3 k ( 1 − 1 1 9 − 5 3 ) → ( 1 0 − 1 2 0 1 − 3 2 ) , γ = k ( 1 3 2 ) 【例 3.9】(2007, 数一、二、三) 设向量组 α 1 α 2 α 3
(A) α 1 − α 2 α 2 − α 3 α 3 − α 1
(B) α 1 + α 2 α 2 + α 3 α 3 + α 1
(C) α 1 − 2 α 2 α 2 − 2 α 3 α 3 − 2 α 1
(D) α 1 + 2 α 2 α 2 + 2 α 3 α 3 + 2 α 1
( α 1 − α 2 , α 2 − α 3 , α 3 − α 1 ) = ( α 1 , α 2 , α 3 ) ∙ ( 1 0 − 1 − 1 1 0 0 − 1 1 )
由| 1 0 − 1 − 1 1 0 0 − 1 1 | = | 1 0 − 1 0 1 − 1 0 − 1 1 | = 0 ∣ α 1 − α 2 , α 2 − α 3 , α 3 − α 1 ∣=∣ α 1 , α 2 , α 3 ∣ ∙ 0 = 0
于是向量组α 1 − α 2 , α 2 − α 3 , α 3 − α 1
令 A = ( α 1 , α 2 , α 3 ) α 1 , α 2 , α 3 r ( A ) = 3
( α 1 + α 2 , α 2 + α 3 , α 3 + α 1 ) = ( α 1 , α 2 , α 3 ) ( 1 0 1 1 1 0 0 1 1 )
因为 | 1 0 1 1 1 0 0 1 1 | = 2 ≠ 0 ( 1 0 1 1 1 0 0 1 1 )
从而 r ( α 1 + α 2 , α 2 + α 3 , α 3 + α 1 ) = r ( α 1 , α 2 , α 3 ) = 3 α 1 + α 2 , α 2 + α 3 , α 3 + α 1
7.设 4 阶矩阵 A = ( a i j ) , a 12 A 12 ≠ 0 , a 1 , a 2 , a 3 , a 4 A , A ∗ A A ∗ x = 0
A. x= k 1 α 1 + k 2 α 2 + k 3 α 3 k 1 , k 2 , k 3
B . x = k 1 α 1 + k 2 α 2 + k 3 α 4 k 1 , k 2 , k 3
C . x = k 1 α 1 + k 2 α 3 + k 3 α 4 k 1 , k 2 , k 3
D . x = k 1 α 2 + k 2 α 3 + k 3 α 4 k 1 , k 2 , k 3
不 可 逆 A 不 可 逆 | A | = 0 r ( A ) < 4 A 12 ≠ 0 r ( A ∗ ) ≠ 0 r ( A ∗ ) = 1 n − r ( A ∗ ) = 3
A 12 ≠ 0 ( α 1 , α 3 , α 4 ) A ∗ A = 0 ( α 1 , α 3 , α 4 )
向量组等价 (1)定义:两个向量组可以互相表示,则两向量组等价
(2)向量组α 1 , α 2 , ⋯ , α m β 1 , β 2 , ⋯ , β s r ( α 1 , α 2 , ⋯ , α m ) = r ( β 1 , β 2 , ⋯ , β s ) = r ( α 1 , α 2 , ⋯ , α m , β 1 , β 2 , ⋯ , β s )
(3)若r ( α 1 , α 2 , ⋯ , α m ) = r ( β 1 , β 2 , ⋯ , β s ) α β β α α 1 , α 2 , ⋯ , α m β 1 , β 2 , ⋯ , β s
(3) 设向量a 1 , a 2 , a 3 k 1 α 1 + k 2 α 2 + k 3 α 3 = 0 , k 1 , k 2 , k 3 k 1 k 3 ≠ 0 a l a 3 B . α 1 , α 2 α 1 , α 3
D . α 1 , α 3 α 2 , α 3
C. α 1 , α 2 α 2 , α 3
( 3 ) C . k 1 α 1 + k 2 α 2 + k 3 α 3 = 0 , k 1 k 3 ≠ 0 , k 2 a 2 α 1 , α 3 α 1 α 3 k 1 k 3 ≠ 0 α 1 α 2 , α 3 α 1 = − k 2 k 1 α 2 − k 3 k 1 α 3 . , α 3 a 1 , a 2 a 2 = α 2 + 0 ∙ α 3 = α 2 + 0 ∙ α 1 α 1 , α 2 α 2 , α 3
列向量组等价 r ( A ) = r ( B ) = r ( A B )
行向量组等价 r ( A ) = r ( B ) = r ( A B )
极大线性无关组 向量组的秩 向量组α 1 , α 2 , ⋯ , α s r ( α 1 , α 2 , ⋯ , α s )
极大无关组的定义 (1)向量组之间线性无关
自由未知量与极大无关组 自由未知量 ==> 基础解系 ==> 非主元列元素
自由未知量 去掉极大无关组(约束未知量),剩下的为自由未知量
自由位置量个数为 系 数 方 程 = n − r ( A ) A 为 系 数 方 程
求向量组的极大线性无关组 (1)将向量按列排成矩阵每层梯子选一列 ,即为极大线性无关组
注:
例:向量组 α 1 = ( 2 , 1 , 3 ) T α 2 = ( 1 , 2 , 1 ) T α 3 = ( 3 , 3 , 4 ) T α 4 = ( 5 , 1 , 8 ) T α 5 = ( 0 , 0 , 2 ) T
( α 1 , α 2 , α 3 , α 4 , α 5 ) = [ 2 1 3 5 0 1 2 3 1 0 3 1 4 8 2 ] ⟶ [ 1 2 3 1 0 2 1 3 5 0 3 1 4 8 2 ] ⟶ [ 1 2 3 1 0 0 − 3 − 3 3 0 0 − 5 − 5 5 2 ] ⟶ [ 1 2 3 1 0 0 1 1 − 1 0 0 0 0 0 2 ] ⟶ [ 1 0 1 3 0 0 1 1 − 1 0 0 0 0 0 1 ]
选取α 1 , α 2 , α 5 α 3 = α 1 + α 2 , α 4 = 3 α 1 − α 2
向量空间 总结:向量空间V中的一个向量组α 1 , α 2 , ⋯ , α r 线 性 无 关 中 每 个 向 量 都 能 由 它 线 性 表 示 { ( 1 ) 线 性 无 关 ( 2 ) V 中 每 个 向 量 都 能 由 它 线 性 表 示 α 1 , α 2 , ⋯ , α r α = x 1 α 1 + x 2 α 2 + ⋯ + x r α r ( x 1 , x 2 , ⋯ , x r ) α α 1 , α 2 , ⋯ , α n β 1 , β 2 , ⋯ , β n { β 1 = c 11 α 1 + c 21 α 2 + ⋯ + c n 1 α n β 2 = c 12 α 1 + c 22 α 2 + ⋯ + c n 2 α n ⋮ β n = c n 1 α 1 + c n 1 α 2 + ⋯ + c n n α n ( β 1 , β 2 , ⋯ , β n ) = ( α 1 , α 2 , ⋯ , α n ) C α 1 , α 2 , ⋯ , α n β 1 , β 2 , ⋯ , β n
方程组 求齐次方程组通解(基础解系) (1)系数矩阵A 行 变 换 → 行 变 换 ( 或 或 100 / 010 / 001 ( n − r = 3 ) 或 10 / 01 ( n − r = 2 ) 或 1 ( n − r = 1 )
【注意】
例题:{ x 1 + 2 x 2 + 3 x 3 + x 4 = 0 2 x 1 − x 2 + x 3 − 3 x 4 = 0 x 1 + x 3 − x 4 = 0
A = [ 1 2 3 1 2 − 1 1 − 3 1 0 1 − 1 ] → r [ 1 2 3 1 0 1 1 1 0 − 2 − 2 − 2 ] → r [ 1 0 1 − 1 0 1 1 1 0 0 0 0 ]
{ x 1 + x 3 − x 4 = 0 x 2 + x 3 + x 4 = 0 k 1 [ − 1 − 1 1 0 ] + k 2 [ 1 − 1 0 1 ] k 1 , k 2 ∈ R
注:“反号顺抄”的原理A X = 0 A → [ 1 0 a 1 b 1 0 1 a 2 b 2 0 0 0 0 ]
同解方程组:{ x 1 + a 1 x 3 + b 1 x 4 = 0 x 2 + a 2 x 3 + b 2 x 4 = 0
⇒ { x 1 = − a 1 x 3 − b 1 x 4 x 2 = − a 2 x 3 − b 2 x 4
(1) x 3 = 1 , x 4 = 0 { x 1 = − a 1 x 2 = − a 2 ⇒ [ x 1 x 2 x 3 x 4 ] = [ − a 1 − a 2 1 0 ] x 3 = 0 , x 4 = 4 { x 1 = − b 1 x 2 = − b 2 ⇒ [ x 1 x 2 x 3 x 4 ] = [ − b 1 − b 2 0 1 ]
注意:必须行最简,行阶梯不能用
基础解系结论 【注意】
【例 4.4】(2011,数一、二) 设 A = ( α 1 , α 2 , α 3 , α 4 ) ( 1 , 0 , 1 , 0 ) T A x = 0 A ∗ x = 0
(A) α 1 , α 2
(B) α 1 , α 3
(C) α 1 , α 2 , α 3
(D) α 2 , α 3 , α 4
由( α 1 , α 2 , α 3 , α 4 ) ( 1 0 1 0 ) = 0 α 1 + α 3 = 0 相 关 α 1 , α 3 相 关 n − r ( A ) = 1 r ( A ) = 3 r ( A ∗ ) = 1 n − r ( A ∗ ) = 3 r ( A ) = 3 为 两 组 极 大 无 关 组 ( α 1 , α 2 , α 4 ) , ( α 2 , α 3 , α 4 ) 为 两 组 极 大 无 关 组 A ∗ A = | A | E = 0 的 每 一 列 都 可 以 由 表 示 A 的 每 一 列 都 可 以 由 A ∗ 表 示 A ∗
故选(D)
已知基础解系反求A 齐次方程基础解系反解 原理:[ ξ 1 ξ 2 ξ 3 ] , [ η 1 η 2 η 3 ] { a 1 x 1 + b 1 x 2 + c 1 x 3 = 0 a 2 x 1 + b 2 x 2 + c 2 x 3 = 0 [ a 1 b 1 c 1 a 2 b 2 c 3 ]
==> [ a 1 b 1 c 1 a 2 b 2 c 3 ] [ ξ 1 η 1 ξ 2 η 2 ξ 3 η 3 ] = 0
转 置 ⇒ 转 置 [ ξ 1 ξ 1 ξ 1 η 2 η 2 η 3 ] [ a 1 a 2 b 1 b 2 c 1 c 2 ] = 0
看成B X = 0 B X = 0 A T A
【步骤】B X = 0
【注意】
例题:已知α 1 = ( 2 , 1 , 1 ) T α 2 = ( 1 , − 2 , − 1 ) T A x = 0 A
B = [ 2 1 1 1 − 2 − 1 ] B X = 0
[ 2 1 1 1 − 2 − 1 ] → [ 1 − 2 − 1 2 1 1 ] → [ 1 0 1 5 0 1 3 5 ]
反 号 顺 抄 ⇒ 反 号 顺 抄 [ − 1 5 − 3 5 1 ]
==>A = [ 1 3 − 5 ]
多加一行可以得到原题的选项:A = [ 1 3 − 5 − 1 − 3 5 ]
再多加n行:A = [ 1 3 − 5 − 1 − 3 5 k 3 k − 5 k ⋮ ]
非齐次方程基础解系反解 总结:已知A X = b ( A | b )
非齐次线性组 A x = b { a 1 x 1 + b 1 x 2 + c 1 x 3 = d 1 a 2 x 1 + b 2 x 2 + c 3 x 3 = d 2
通解为 k 1 [ ξ 1 ξ 2 ξ 3 ] + k 2 [ η 1 η 2 η 3 ] + [ λ 1 λ 2 λ 3 ]
{ a 1 x 1 + b 1 x 2 + c 1 x 3 = 0 a 2 x 1 + b 2 x 2 + c 3 x 3 = 0
令非齐次方程组 { a 1 x 1 + b 1 x 2 + c 1 x 3 = d 1 a 2 x 1 + b 2 x 2 + c 2 x 3 = d 2 [ λ 1 λ 2 λ 3 ] d 1 , d 2
【例题】k 1 ( 1 , 1 , 0 , 0 ) T + k 2 ( 1 , 0 , 2 , 1 ) T + ( 1 2 , 0 , 1 2 , 0 ) T , k 1 k 2 ∈ R A x = b
(1)先求齐次方程组[ 1 1 0 0 1 0 2 1 ] → [ 1 0 2 1 0 1 − 2 − 1 ]
负 号 顺 抄 ⇒ 负 号 顺 抄 [ − 2 2 1 0 ] , [ − 1 1 0 1 ]
A X = 0 A = [ − 2 2 1 0 − 1 1 0 1 ]
为 A x = 0 为 { − 2 x 1 + 2 x 2 + x 3 = 0 − x 1 + x 2 + x 4 = 0
令A x = b { − 2 x 1 + 2 x 2 + x 3 = b 1 − x 1 + x 2 + x 4 = b 2
代入:[ 1 2 0 1 2 0 ] T
即:A x = b { − 2 x 1 + 2 x 2 + x 3 = − 1 2 − x 1 + x 2 + x 4 = − 1 2
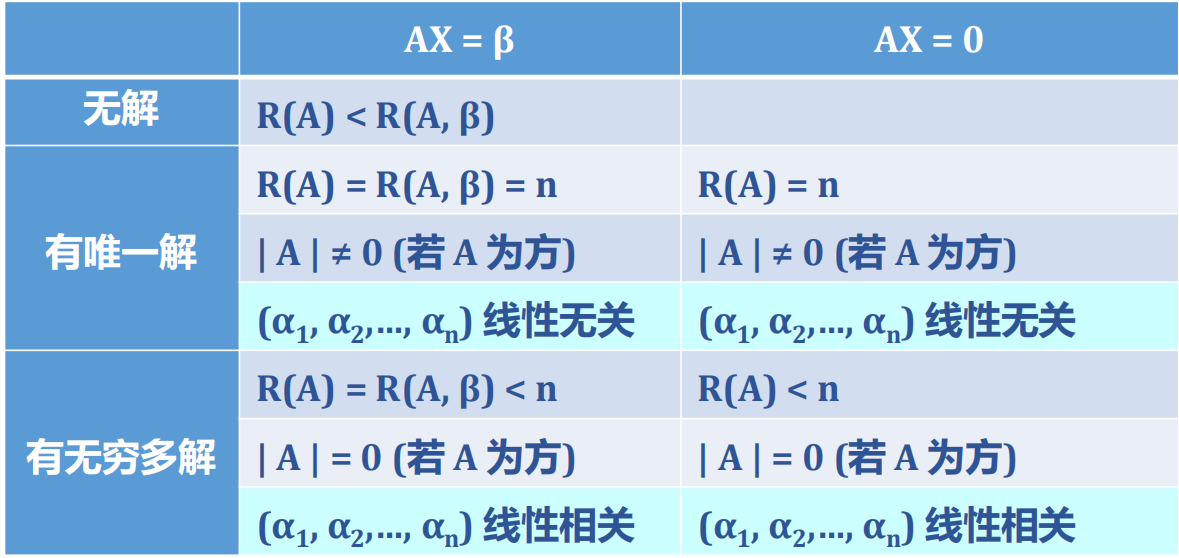
线性方程组解的判定 (1)A X = 0 A X = b A X = 0 A X = 0 r ( A ) = n | A | ≠ 0
② A X = 0 r ( A ) < n | A | = 0
(4)A X = b A X = b r ( A ) ≠ r ( A | b ) r ( A ) + 1 = r ( A | b ) | A | = 0
② A X = b r ( A ) = r ( A | b ) = n | A | ≠ 0 A X = b A X = 0
③ A X = b r ( A ) = r ( A | b ) < n | A | = 0 A X = 0
【总结】线性方程组解的情况的判断
【例 4.1】(2001, 数三) 设 A n α n r ( A α α T 0 ) = r ( A )
(A) A x = α
(B) A x = α
(C) ( A α α T 0 ) ( x y ) = 0
(D) ( A α α T 0 ) ( x y ) = 0
对(C)(D)r ( A α α T 0 ) = r ( A ) < n + 1
对(A)(B)r ( A ) ≤ r ( A α ) ≤ r ( A α α T 0 ) = r ( A ) r ( A ) = r ( A α ) A X = α
(5) 设矩阵A = ( 1 1 1 1 2 a 1 4 a 2 ) b = ( 1 d d 2 ) Ω = { 1 , 2 } Ax = b
(A) a ∉ Ω , d ∉ Ω .
(B) a ∉ Ω , d ∈ Ω .
(C) a ∈ Ω , d ∉ Ω .
(D) a ∈ Ω , d ∈ Ω .
解的结构 (1)设α 1 , α 2 , ⋯ , α n A X = 0 k 1 α 1 + k 2 α 2 + ⋯ + k n α n A X = 0 k 1 , k 2 , ⋯ , k n η 1 , η 2 , ⋯ , η n A X = b 是 的 解 是 的 解 k 1 η 1 + k 2 η 2 + ⋯ + k n η n { 是 A X = 0 的 解 , k 1 + k 2 + ⋯ + k n = 0 是 A X = b 的 解 , k 1 + k 2 + ⋯ + k n = 1 η 1 − η 2 A X = 0 η 1 , η 2 , ⋯ , η n A X = b η 2 − η 1 , η 3 − η 1 , ⋯ , η n − η 1 A X = 0 n − 1 η A X = b α A X = 0 η + α A X = b A X = 0 n − r ( A ) A X = 0 α 1 , α 2 , ⋯ , α n A X = 0 k 1 α 1 + k 2 α 2 + ⋯ + k n α n A X = 0 A X = b 齐 次 通 解 非 齐 特 解 x = 齐 次 通 解 + 非 齐 特 解
(2011,数三)设A 4 × 3 η 1 , η 2 , η 3 A x = β k 1 , k 2 A x = β
( A ) η 2 + η 3 2 + k 1 ( η 2 − η 1 ) ( B ) η 2 − η 3 2 + k 2 ( η 2 − η 1 ) ( C ) η 2 + η 3 2 + k 1 ( η 2 − η 1 ) + k 2 ( η 3 − η 1 ) ( D ) η 2 − η 3 2 + k 1 ( η 2 − η 1 ) + k 2 ( η 3 − η 1 )
(2002,数一、二、三)设A = ( α 1 , α 2 , α 3 , α 4 ) α 2 , α 3 , α 4 α 1 = 2 α 2 − α 3 β = α 1 + α 2 + α 3 + α 4 A x = β
无 关 α 2 , α 3 , α 4 无 关 r ( A ) ≥ 3 α 1 = 2 α 2 − α 3 r ( A ) = 3 基 础 解 系 个 数 : 基 础 解 系 个 数 : n − r ( A ) = 1 α 1 − 2 α 2 + α 3 A ( 1 − 2 1 0 ) = 0 β = α 1 + α 2 + α 3 + α 4 A ( 1 1 1 1 ) = 0
==> x = k ( 1 − 2 1 0 ) + ( 1 1 1 1 )
【例 4.8】(2017, 数一、二、三) 设 3 阶矩阵 A = ( α 1 , α 2 , α 3 ) α 3 = α 1 + 2 α 2
(I) 证明 r ( A ) = 2
(II) 若 β = α 1 + α 2 + α 3 A x = β
(I) α 3 = α 1 + 2 α 2 r ( A ) < 3 A ∼ ( λ 1 λ 2 λ 3 ) λ 1 ≠ λ 2 ≠ λ 3 若 则 若 λ 1 = 0 , 则 λ 2 ≠ 0 , λ ≠ 0 r ( A ) = r ( Λ ) = 2
(II) 同上道例题理
【例 18】设 4 阶矩阵 A = ( α 1 , α 2 , α 3 , α 4 ) α 1 , α 2 , α 3 α 2 , α 3 , α 4 ξ = ( 1 , 2 , 3 , a ) T A x = 0
(I) 求 a
(II) 若 η = ( 2 , b , c , d ) T A x = β β = α 1 + α 2 + α 3 + α 4 b , c , d
【详解】(I) 由 α 2 , α 3 , α 4 α 2 , α 3 α 1 , α 2 , α 3 α 1 α 2 , α 3
由 ( α 1 , α 2 , α 3 , α 4 ) ( 1 2 3 a ) = 0 α 1 + 2 α 2 + 3 α 3 + a α 4 = 0 a = 0
若 a ≠ 0 α 2 , α 3 , α 4
(II)x = k ( 1 2 3 0 ) + ( 1 1 1 1 ) { b = 3 c = 4 d = 1
【例4.7】设A为4阶矩阵,k为任意常数,η 1 η 2 η 3 A x = b η 1 + η 2 = ( 1 2 3 4 ) η 2 + 2 η 3 = ( 2 3 4 5 ) r ( A ) = 3 A x = b
(A) ( 1 2 3 4 ) + k ( − 1 0 1 2 )
(B) ( 2 3 4 5 ) + k ( 1 2 0 1 )
(C) ( 0 1 2 3 ) + k ( − 1 0 1 2 )
(D) ( 1 1 1 1 ) + k ( 1 2 0 1 )
选(C)
AB=0的三个角度 (1) r ( A ) + r ( B ) ≤ n A m × n B n × s = 0
(2)A X = 0
证明(2.1):A B = 0 ⇒ A ( β 1 , β 2 , ⋯ , β n ) = 0 ⇒ ( A β 1 , A β 2 , ⋯ , A β n ) = 0
证明(2.2);是 的 解 x = [ x 1 x 2 x 3 ] 是 A X = 0 的 解 A [ x 1 x 2 x 3 ] = 0 = [ 0 0 0 ] [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ x 1 x 2 x 3 ] = 0 = [ 0 0 0 ]
(3)B ≠ 0 又 r ( A ) + r ( B ) ≤ n , 又 r ( B ) ≥ 1 ⇒ r ( A ) ≤ n − 1 的 列 向 量 组 线 性 相 关 r ( A m × n ≤ n − 1 ⇒ A 的 列 向 量 组 线 性 相 关 A ≠ 0
【例题】9.设A A ∗ A A ( A − A ∗ ) = O A ≠ A ∗ r ( A )
(A)0或1
(B)1或3
(C)2或3
(D)1或2
r ( A ) + r ( A − A ∗ ) ≤ 4 , r ( A − A ∗ ) ≥ 1 r ( A ) = 1 , 2 , 3 A 2 − A A ∗ = 0 A 2 − | A | E = 0 A 2 = 0 r ( A ) + r ( A ) ≤ 4 或 r ( A ) = 1 或 2
AB=E 长得差不多放一起
A B = E A A − 1 = E 满 秩 可 交 换 A , B 满 秩 , 可 交 换
【例1】设n A B A 2 − A B = E r ( A B − B A + 2 A ) =
答案:n
【例2】(5) 设n阶方阵A,B,C满足关系式ABC=E,其中E是n阶单位阵,则必有
(5)【答案】(D).
【解】由A B C = E B C = A − 1 B C A = A − 1 A = E
AB=C 【例 3.2】(2013, 数一、二、三) 设 n 阶矩阵 A, B, C 满足 AB = C, 且 B 可逆, 则【 】
(A) C 的行向量组与 A 的行向量组等价
(B) C 的列向量组与 A 的列向量组等价
(C) C 的行向量组与 B 的行向量组等价
(D) C 的列向量组与 B 的列向量组等价
A B = C A = C B − 1
同解方程组 什么是同解方程组 { x 1 + 2 x 2 − x 3 + x 4 = 6 2 x 1 − x 2 + x 3 − x 4 = − 1 [ 1 2 − 1 1 6 2 − 1 1 − 1 − 1 ]
{ x 1 + 2 x 2 − x 3 + x 4 = 6 − 5 x 2 + x 3 − 3 x 4 = − 13 [ 1 2 − 1 1 6 0 − 5 3 − 3 − 13 ]
上式与下式的区别是做了一次初等行变换,它们的解是一样的,它们显然是同解方程组!
齐次方程组同解 齐次方程组 A X = 0 B X = 0
<==> A可经过有限次初等行变换到B∃ P P A = B r ( A ) = r ( B ) = r [ A B ] A X = 0 B X = 0
【注意】A X = 0 B X = 0 r ( A ) = r ( B ) = r [ A B ] A X = 0 B X = 0 A T A = 0 A X = 0 A X = 0 P A X = 0 A n X = 0 A n + 1 = 0 与 同 解 ( A 3 X = 0 与 A 4 X = 0 同 解 )
非齐次方程组同解 非齐次方程组A X = α B X = β ( A | α ) ( B | β )
<==> ( A | α ) ( B | β ) r ( A | α ) = r ( B | β ) = r ( A α B β )
齐次方程组同解的结论 A X = 0 B X = 0 A X = 0 B X = 0 A X = 0 B X = 0 n − r ( A ) = n − r ( B ) r ( A ) = r ( B ) A X = 0 B X = 0 A X = 0 ( A X = 0 B X = 0 ) r ( A ) = r ( A B ) r ( A ) ≥ r ( B ) 👉️同解的充要命题,A X = 0 B X = 0 r ( A ) = r ( B ) = r ( A B ) 若A X = 0 B X = 0 r ( A ) = r ( B ) A X = 0 B X = 0 由(2)可知,若想证明r ( A ) = r ( B ) A X = 0 B X = 0 设 3 阶矩阵 A = ( α 1 , α 2 , α 3 ) B = ( β 1 , β 2 , β 3 ) α 1 , α 2 , α 3 β 1 , β 2 , β 3
(A) A X = 0 B X = 0
(B) A T X = 0 B T X = 0
(C) B X = 0 A X = 0
(D) B T X = 0 A T X = 0
【法一】 A 可由 B线性表出 <==> r ( B ) = r ( B A ) r ( A ) = r ( A B ) r ( A T ) = r ( A T B T ) r ( B ) = r ( B A ) r ( B T ) = r ( B T A T )
r ( B ) = r ( B A ) r ( B T ) = r ( B T A T )
【法二】B P = A { B X = 0 A X = 0 B P X 0 = 0 B X 0 = 0 { B T X = 0 P T B T X = 0 P T B T X 0 = 0 B T X 0 = 0 { B X = 0 A X = 0 B X 0 = 0 B P X 0 = 0 { B T X = 0 P T B T X = 0 B T X 0 = 0 P T B T X 0 = 0
选(D)
设矩阵 A = ( 0 1 a 1 0 1 ) B = ( 1 1 1 1 b 2 ) f ( x 1 , x 2 , x 3 ) = x T B A x
已知方程组 A x = 0 B T x = 0 a , b x = Q y f ( x 1 , x 2 , x 3 )
(I)A x = 0 B T x = 0 r ( A ) = r ( A B T ) = 2 > r ( B ) r ( B ) = 1
==> a = 1 , b = 2
(II)
C = B A = [ 1 1 2 1 1 2 2 2 4 ] λ 1 = 0 , λ 2 = 0 , λ 3 = 6 与 正 交 α 1 = ( 1 , 1 , − 1 ) T , α 2 = ( 1 , − 1 , 0 ) T α 1 与 α 2 正 交 α 3 = ( i j k 1 1 − 1 1 − 1 0 ) = ( 1 , 1 2 ) T
==>正交化:e 1 = 1 3 ( 1 , 1 , − 1 ) T , e 2 = 1 2 ( 1 , − 1 , 0 ) T , e 3 = 1 6 ( 1 , 1 2 ) T
==> Q = ( e 1 , e 2 , e 3 ) = [ − 1 2 − 1 3 1 6 1 2 − 1 3 1 6 0 1 3 2 6 ]
(5) 设A n ( n ⩾ 2 ) , B n , b n A x = b A B x = b
( B) 若方程组A x = b B A x = b
( C) 若方程组A x = 0 A B x = 0
( D) 若方程组A x = 0 B A x = 0
【例24】设A,B为n阶方阵, 若线性方程组Ax=0的解均为Bx=0的解, 则下列方程组与Ax=0同解的个数为【】
①(A+B)x=0 ②ABx=0 ③BAx=0 ④(A-B)(A+B)x=0 ⑤(A)(B)x=0
(A) 1 (B) 2 (C) 3 (D) 4
【详解】令B=-A, 排除①; 令B=O, 排除②、③.
由Ax=0的解都是Bx=0的解, 知Ax=0与(A)(B)x=0同解.
又( A − B A + B ) ( A B ) ( A B ) x = 0 ( A − B A + B ) x = 0
线性代数中答案不唯一的情况 (1)A X = 0 A X = b A A X = b P , Q
线代小题综合
设A为3阶实对称矩阵,A的各行元素之和均为0,若A的全部非零特征值为1,6,则下列命题中,正确的个数为()
① A ∗ 0
②( A ∗ ) ∗ ≠ O
③ 6 A ∗
④ A ∗ x = 0 A x = 0
设n A A ∗ ≠ O , ξ 1 , ξ 2 , ξ 3 , ξ 4 A x = b A x = b
A ∗ ≠ 0 或 r ( A ) = n 或 n − 1 有 四 个 解 A x = b 有 四 个 解 r ( A ) = r ( A ― ) = n − 1 n − r ( A ) + 1 = 2
设 3 阶非零矩阵A A 2 = O A x = b A x = b
r ( A ) + r ( A ) ≤ 3 r ( A ) ≤ 1 有 解 A x = b 有 解 r ( A ) ≠ 0 r ( A ) = 1 n − r ( A ) + 1 = 3
(4)设A n P n n α A λ ( P − 1 A P ) T λ
(A)P − 1 α
( B)P T α
( D)( P − 1 ) T α
(C)P α
有:A α = λ α A T α = λ α
( P − 1 A P ) T β = λ β P T A T ( P − 1 ) T β = λ β A T ( P − 1 ) T β = λ ( P − 1 ) T β
==> ( P − 1 ) T β = α β = P T α
(7) 设 A α A α = 0 β T α = 0 β A β = β
A. A 3
B. A 3
C. A 2
D. A 2
β T α = 0 α T β = 0 n − r ( α ) = 2 β 1 , β 2 A β 1 = β 1 , A β 2 = β 2 λ 1 = λ 2 = 1 A α = 0 λ 3 = 0
(A) A 3 1 3 , 1 3 , 0 t r ( A 3 ) = 2
设A B AB = O A + E B | tr ( A ) | + | tr ( B ) | =
A B = 0 r ( A ) + r ( B ) ≤ 3 且 r ( A ) > 0 且 r ( B ) > 0 的 特 征 值 : A 的 特 征 值 : λ 1 , λ 2 , 0 的 特 征 值 : A + E 的 特 征 值 : λ 1 + 1 , λ 2 + 1 , 1 的 特 征 值 : B 的 特 征 值 : λ 1 + 1 , λ 2 + 1 , 1
当λ 1 + 1 = 0 的 特 征 值 : A 的 特 征 值 : − 1 , λ 2 , 0 的 特 征 值 : B 的 特 征 值 : 0 , λ 2 + 1 , 1
当λ 2 = 0 的 特 征 值 : A 的 特 征 值 : − 1 , 0 , 0 的 特 征 值 : B 的 特 征 值 : 0 , 1 , 1 | t r ( A ) | + | t r ( B ) | = 3
当λ 2 + 1 = 0 的 特 征 值 : A 的 特 征 值 : − 1 , − 1 , 0 的 特 征 值 : B 的 特 征 值 : 0 , 0 , 1 | t r ( A ) | + | t r ( B ) | = 3
综上,答案为3
(10) 设 A, B 为 2 阶矩阵, 且 AB=BA, 则 “A 有两个不相等的特征值” 是 “B 可对角化”的
A. 充分必要条件.
B. 充分不必要条件.
C. 必要不充分条件.
D. 既不充分也不必要条件.
必要性:A = B = E 的 特 征 值 均 为 A 的 特 征 值 均 为 1
充分性:{ A α 1 = λ 1 α 1 A α 2 = λ 2 α 2
==> B A α 1 = λ 1 B α 1 A B α 1 = λ 1 B α 1 时 为 的 特 征 向 量 时 为 的 特 征 值 的 特 征 向 量 { B α 1 = 0 时 α 1 为 B 的 特 征 向 量 B α 1 ≠ 0 时 B α 1 为 A 的 特 征 值 λ 1 的 特 征 向 量
==> B α 1 = k α 1 仍 为 的 特 征 向 量 α 1 仍 为 B 的 特 征 向 量
综上,为 的 特 征 向 量 α 1 为 B 的 特 征 向 量
同理可得,为 的 特 征 向 量 α 2 为 B 的 特 征 向 量
与 α 1 与 α 2
线代大题 【例题1】阶 矩 阵 3 阶 矩 阵 A = ( α 1 , α 2 , α 3 ) α 1 + α 3 = 0 , α 1 − α 2 = 0 X = ( x 1 , x 2 , x 3 ) T ( x 1 , x 2 , x 3 ) = x T A x
α 1 = − α 3 , α 1 = α 2 A = [ x x − x y y − y z z − z ]
每行元素和为1 ==> [ 1 1 − 1 1 1 − 1 1 1 − 1 ]
A不对称,将A对称化:B = A + A T 2 = [ 1 1 0 1 1 0 0 0 − 1 ]
| λ E − B | = | λ − 1 − 1 0 − 1 λ − 1 0 0 0 λ + 1 | = ( λ + 1 ) ( λ − 2 ) λ
【特征值验算技巧】t r ( A ) = ∑ λ i t r ( B ) = 1 + 1 − 1 = 1 = − 1 + 2 + 0
设A = ( a i j ) n ( n ≥ 3 ) A i j a i j
(I)a i j = A i j ( i , j = 1 , 2 , ⋯ , n ) ⇔ A ∗ = A T ⇔ A A T = E | A | = 1 ;
(II)a i j = − A i j ( i , j = 1 , 2 , ⋯ , n ) ⇔ A ∗ = − A T ⇔ A A T = E | A | = − 1.
(I)A ∗ = A T | A ∗ | = | A | n − 1 = | A T | = | A | | A | = 0 , 1 , − 1 | A | = a 11 A 11 + ⋯ a 1 n A 1 n = a 11 2 + ⋯ + a 1 n 2 > 0 | A | = 1 A A T = A A ∗ = | A | E = E
(II)A ∗ = − A T
【记住推导过程即可】
【2021,数一】设 A = ( a 1 − 1 1 a − 1 − 1 − 1 a )
(I) 求正交矩阵 P,使得 P T A P
(II) 求正定矩阵 C,使得 C 2 = ( a + 3 ) E − A
(I)A = [ 1 1 − 1 1 1 − 1 − 1 − 1 1 ] + ( a − 1 ) E
λ 3 = 3 , λ 1 = λ 2 = 0 α 1 = ( − 1 1 0 ) x 1 + x 2 − x 3 = 0 α 2 = ( 1 1 2 ) α 3 = α 1 × α 2 = ( − 1 − 1 , 1 ) P = [ η 1 η 2 η 3 ] = [ − 2 2 6 6 − 3 3 2 2 6 6 − 3 3 0 6 3 3 3 ] P T A P = [ a − 1 0 0 0 a − 1 0 0 0 a + 2 ] P
(2) 由(1)知, ( a + 3 ) E − A = ( a + 3 ) E − P [ a − 1 0 0 0 a − 1 0 0 0 a + 2 ] P ⊤ = P [ 4 0 0 0 4 0 0 0 1 ] P ⊤ .
令 C = P [ 2 0 0 0 2 0 0 0 1 ] P ⊤ C 2 = ( a + 3 ) E − A
C = [ − 2 2 6 6 − 3 3 2 2 6 6 − 3 3 0 6 3 3 3 ] [ 2 0 0 0 2 0 0 0 1 ] [ − 2 2 6 6 − 3 3 2 2 6 6 − 3 3 0 6 3 3 3 ] T = [ 5 3 − 1 3 1 3 − 1 3 5 3 1 3 1 3 1 3 5 3 ] .