数字信号处理

傅里叶变换

前置知识

公式一：计算原向量投影后的坐标

即：

表示在向量u在i坐标系下的坐标。

\begin{bmatrix} \end

公式二：用新的基函数和坐标复原原向量

即：

空间坐标变换总结

1. 坐标系中的基向量，由两两正交（内积为零）且长度为1的n（n为空间维度）个向量组成。
2. 坐标系中任意一个向量可表示为基向量的线性组合，其系数即为坐标。
3. 向量丛一个坐标系变换到另一个坐标系，需要求向量在新坐标系的每个基向量的投影。

向量的内积（投影）

其他补充文章：👉️向量的内积外积与其几何意义👈️ 假设有一个k维的向量u，这个k维向量在某个基向量上的投影为：

一般来说有因为为基向量，故有(3)式成立

那么如果把向量的维度看作成数组，就可以计算两数组之间的内积。
如果把数组中n的间隔逐渐变得密集，就可以看作成函数，从而计算两函数之间的内积。

函数内积(两个无穷维向量的投影)

参考链接：

将(4)式理解成对应点的值相乘再求和的极限形式

当取值密度趋向于无穷大时，得到(4)式积分形态

积分变换

第一章 绪论

四种信号类型

1. 连续时间信号
2. 离散时间信号
3. 模拟信号
4. 数字信号

信号类型	时间	幅度
连续时间信号	连续	可连续、可离散
离散时间信号	离散	可连续、可离散
模拟信号	连续	连续
数字信号	离散	离散

三种频率的关系

1. 模拟频率
2. 模拟角频率
3. 数字频率

1. 模拟信号$x_a(t) = Acos(2\pi ft+\phi) $
2. 模拟频率
3. 模拟角频率
4. 数字信号
5. 数字频率
6. 采样周期 <==> 采样率

数字频率、模拟角频率和模拟频率的关系为

第二章 离散时间信号与系统

奈奎斯特采样定理

若是带限信号，要想采样后的信号能够不失真地还原出原信号，则采样频率必须大于信号最高频率分量的两倍。
条件：

1. 带宽有限
2. 理想采样

tip: 采样频率， 信号最高频率

---

这是一个分割线~

---

例题：的最高频率为8kHz，则对3、、分别进行采样时需要的最低采样频率为？

解得：

解得：

解得：

---

这是一个分割线~

---

结论：

实际采样与理想采样的异同

本质不同 ==> 采样序列不同：采样序列由单位冲激串变为矩形脉冲串
相同点：周期延拓仍为
不同点：幅度加权因子由 ==>

插值重构

理想低通滤波器的截止频率满足：
tip: 采样频率， 信号最高频率

典型序列

1.矩形序列

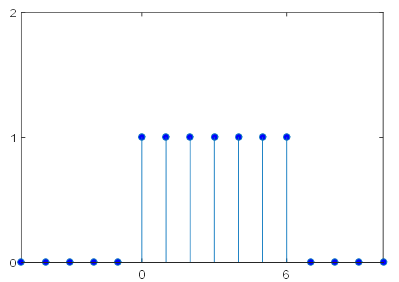
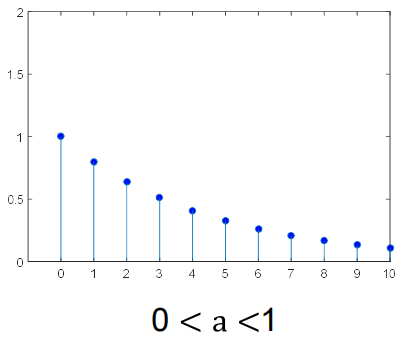
2.实指数序列

3.复指数序列

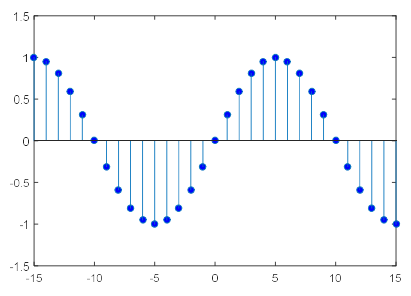
4.正弦型序列

序列的周期性

定义：如果对于所有的n，存在一个最小的正整数N ,下列等式成立

则称序列x(n)为周期序列，其周期为N。

---

这是一个分割线~

---

例题：计算的周期 法1： 积化和差分解成相加形式：

找最小公倍数，对第一个sin有：

对第二个sin有：

解得：周期为15

序列运算

卷积：
1.有限长序列：
使用冲激法计算卷积
写了一个简陋的冲激法实现，仅供理解

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 100010;

int a[N], b[N];
int n, m;
int ans[N];

int main()
{
	cin >> n;
	for(int i = 0; i < n; i ++) cin >> a[i];
	cin >> m; 
	for(int i = 0; i < m; i ++) cin >> b[i];
	for(int i = 0; i < n; i ++)
	{
		for(int j = 0; j < m; j ++)
		{
			ans[i + j] += a[i] * b[j];
			cout << a[i] * b[j] << ' ';
		} 
		cout << endl;
	}
	for(int i = 0; i < n + m - 1; i ++) cout << ans[i] << ' ';
	return 0; 
}
//目的：计算{1, 1, 2}0 * {1, 2, 3, 4}0
//输入
//3
//1 1 2
//4
//1 2 3 4
//结果
//1 2 3 4
//  1 2 3 4
//    2 4 6 8
//1 3 7 11 10 8

系统性质

1. 线性：输入为线性组合 ==> 输出同线性组合

2. 时不变：输入时延 ==> 输出同时延

3. 因果 常用判定：系统输出仅与当前或过去值有关
   LTI独有判定：满足 或 收敛域向外的，包括 则是因果系统
4. 稳定 常用判定：有限输入 ==> 有限输出
   LTI独有判定：满足有限 或 收敛域包含单位圆 则是稳定系统

Tips: 就是将所有的变为
就是将所有的 变为

LTI(Linear Time-invarient)系统 线性时不变系统
性质：
存在冲激响应，系统函数

输入为冲激序列时，输出为冲激响应

DTFT

1.定义：
正变换：

反变换：

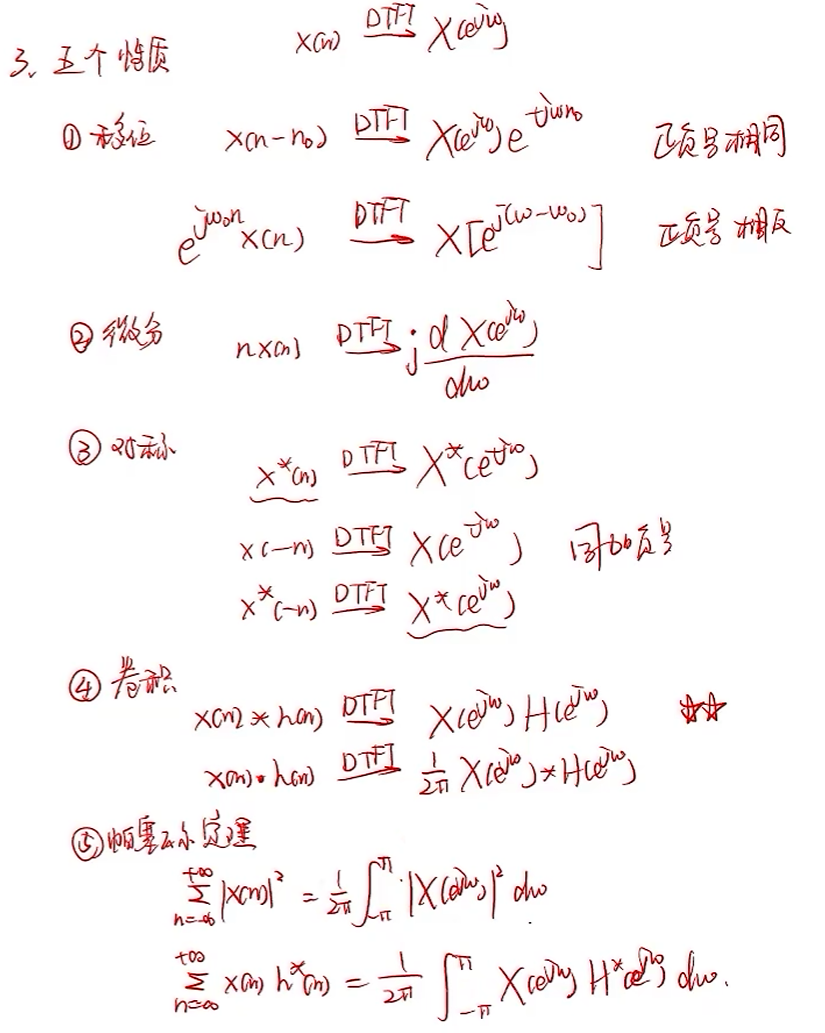
Z变换

1.定义：
正变换：

收敛域：

第三章 离散傅里叶变换

DFS

正变换：

反变换：

DFT

正变换：

反变换：

圆周卷积

N点圆周卷积：

计算方法：
1.先算线性卷积 2.再剪断，补充相加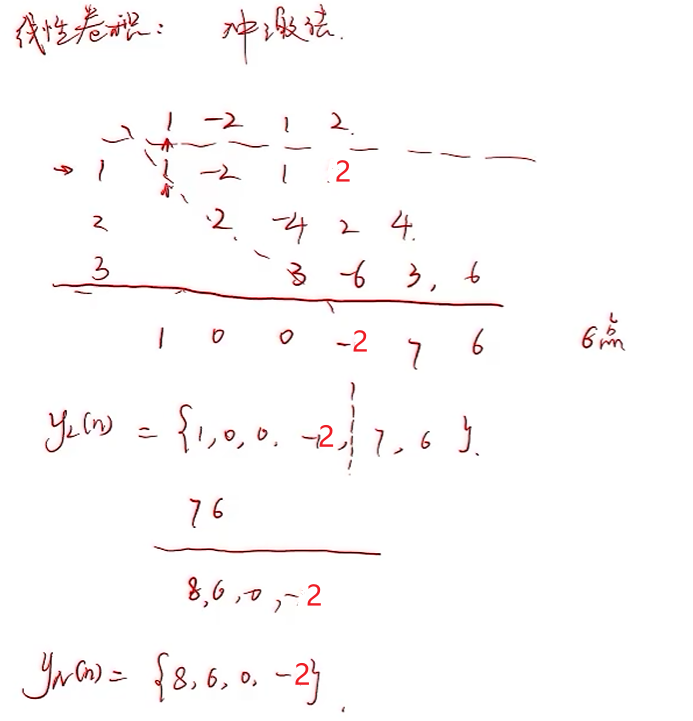

第四章 DFT应用

重叠相加法与重叠保留法

直接上例题：
序列x(n)={1,2,3,4,5,6,7,8,9,10}0，h(n)={1,2,-1}0，请利用重叠相加法计算x(n)和h(n)的线性卷积结果。

长度为10,长度为3,可把按照进行分段,

计算各段线性卷积结果，

---

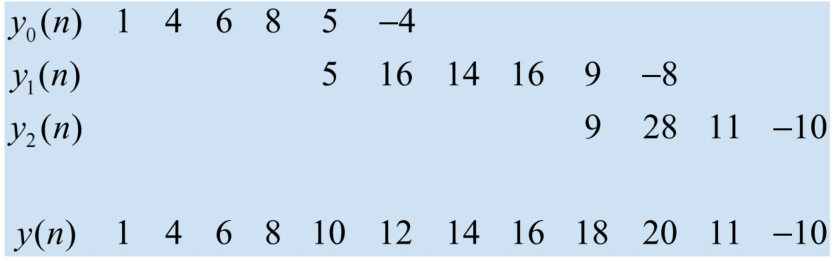
这是一个分割线~

---

请利用重叠保留法重新计算。

把按照进行分段，前后数据段重叠长度为，并且在第1段数据前补2个零值，

计算各段圆周卷积结果

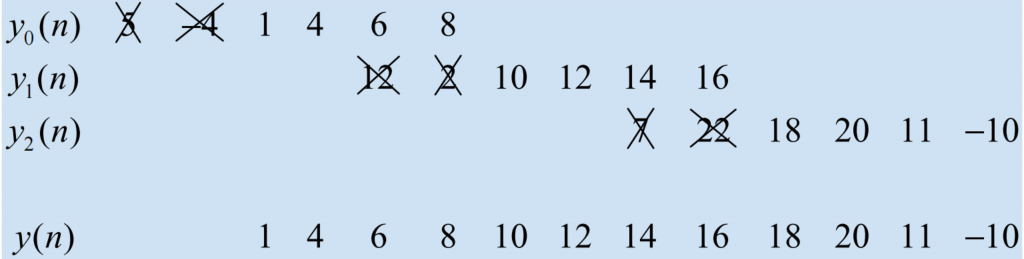
第五章 FFT

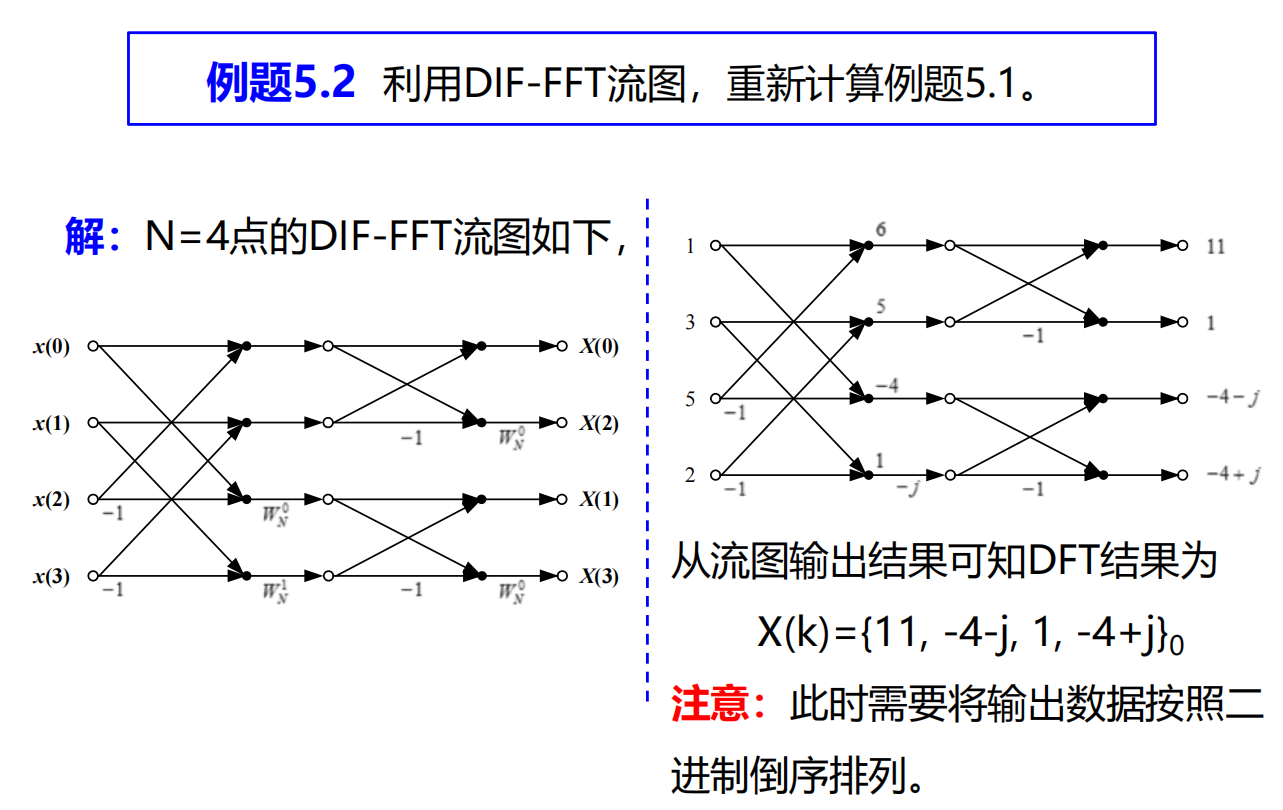
DIT-FFT

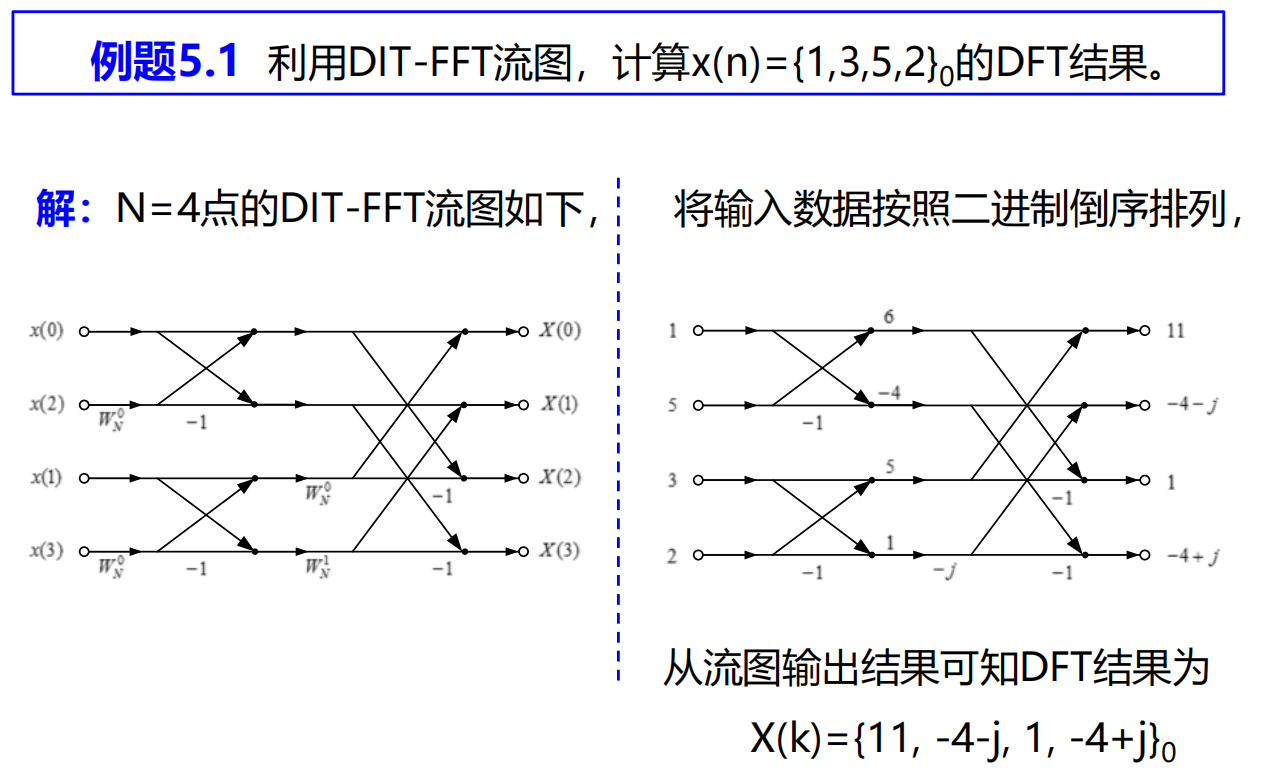
DIF-FFT

第六章 IIR数字滤波器的设计

脉冲响应不变法求解系统函数

两个重要结论：

双线性变换法求解系统函数

记住变换公式即可：

第七章 FIR数字滤波器的设计

线性相位

第一类线性相位：
第二类线性相位：

四类线性相位FIR数字滤波器特点

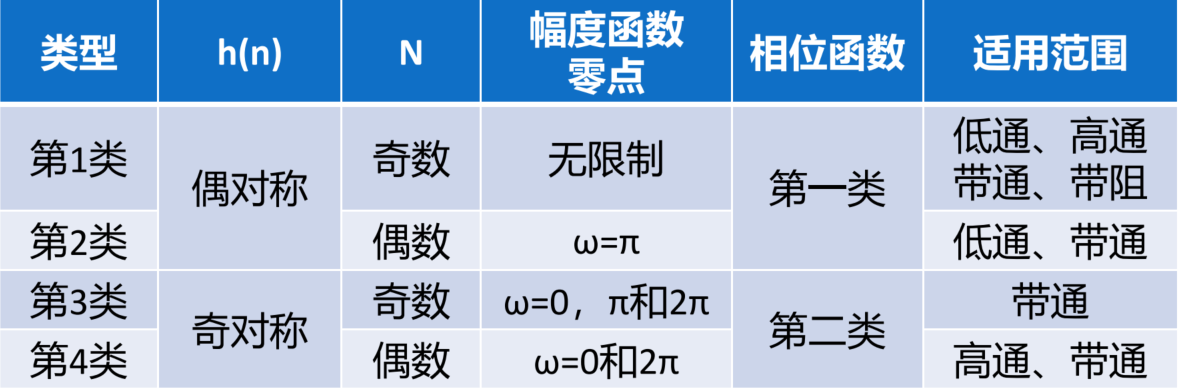
滤波器类型、幅度函数和相位函数

类型	h(n)	N	低通	高通	带通	带阻
第1类	偶	奇	√	√	√	√
第2类	偶	偶	√	×	√	×
第3类	奇	奇	×	×	√	×
第4类	奇	偶	×	√	√	×

窗函数设计法

1. 根据具体需求，确定FIR数字滤波器技术指标；
2. 根据阻带最小衰减，确定窗函数类型；
3. 根据过渡带宽，确定窗函数长度；
4. 确定窗函数和理想滤波器；
5. 计算实际滤波器单位脉冲响应;
6. 验证实际滤波器是否满足设计指标。

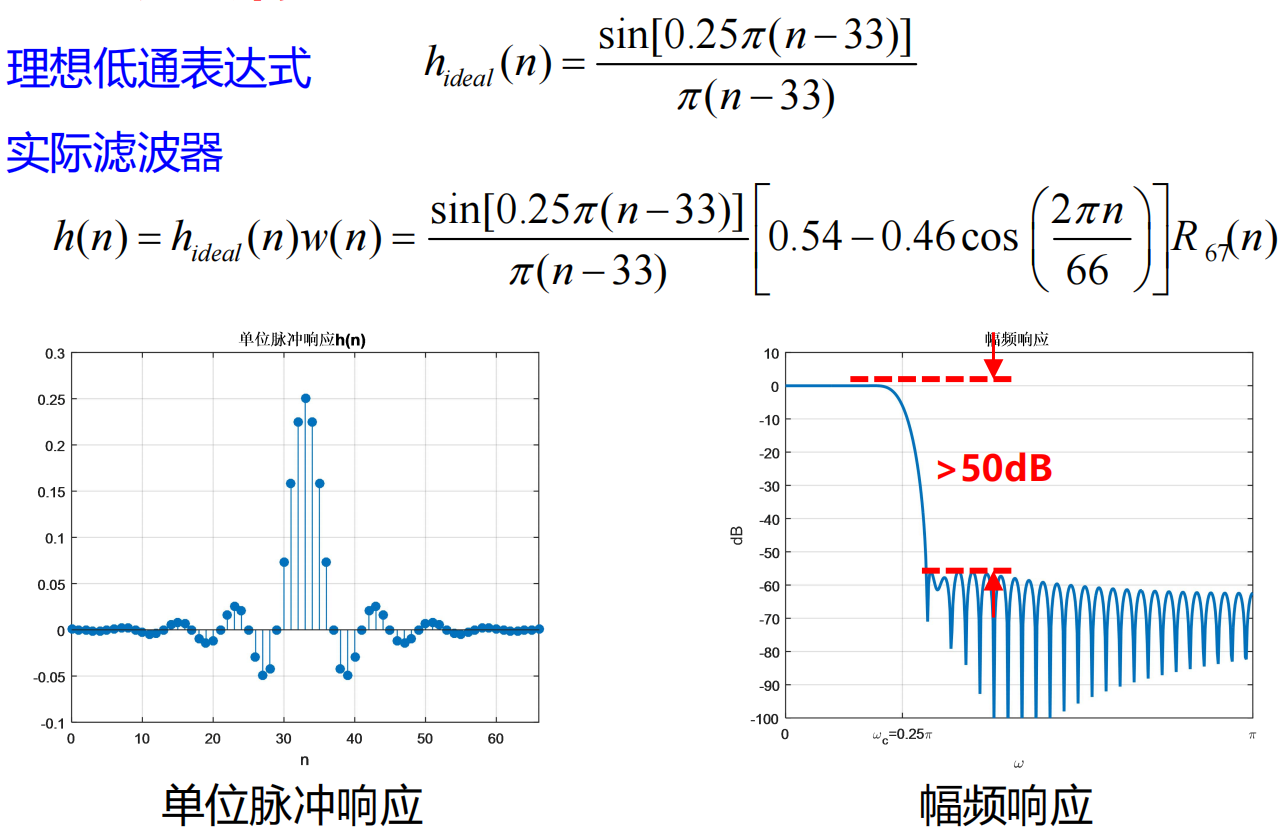
频率采样设计法

1：对理想滤波器的频率响应等间隔采样，

2：将采样值作为实际FIR滤波器频率响应样本值。

3：对H(k)进行IDFT，将得到的N点h(n)作为实际FIR滤波 器的单位脉冲响应，