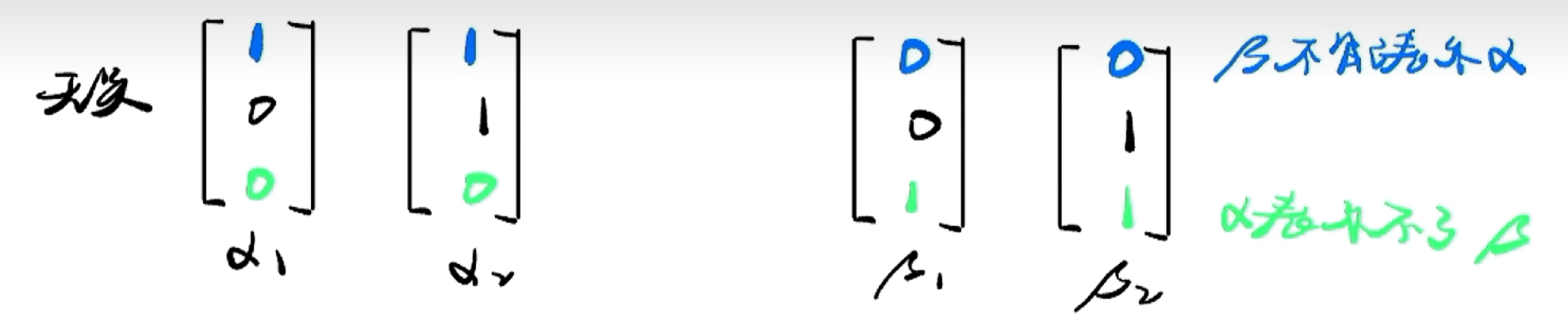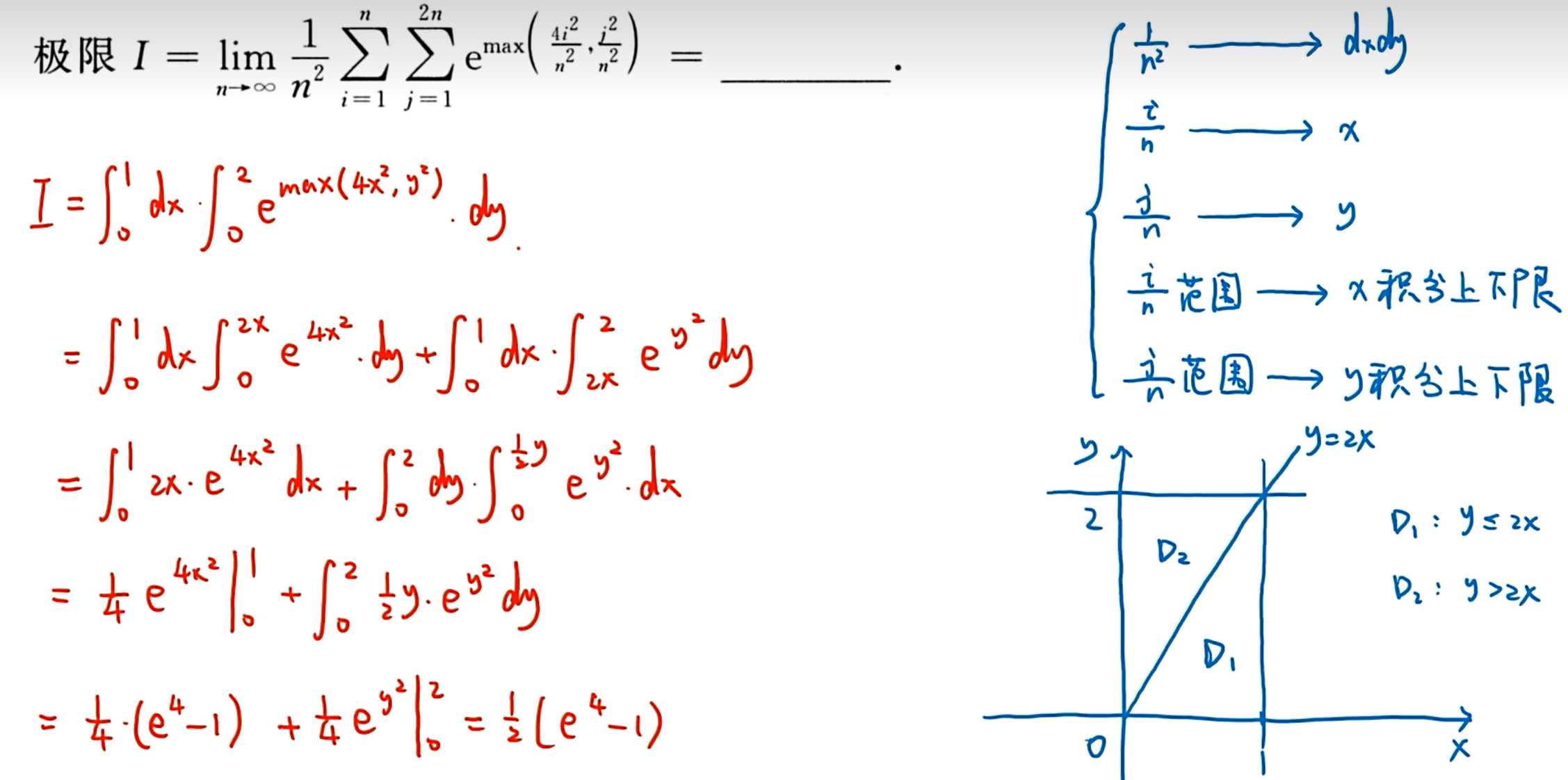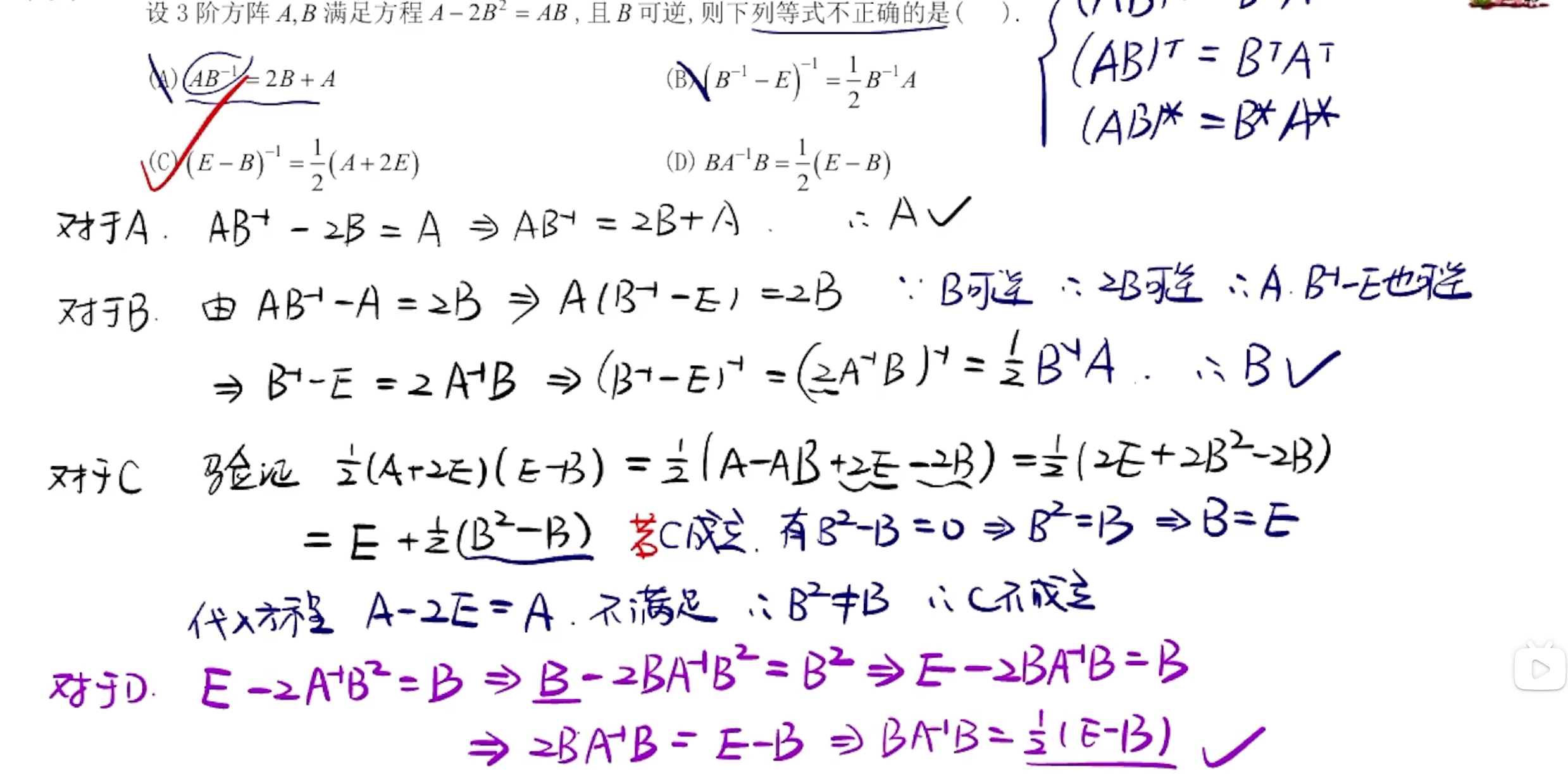上官呆呆的笔记

Appearance

错题本 ​

好题 ​

考察极限存在 ​

难度评级：⭐️

若极限

存在，求a的取值范围与此极限的值。

点击展开答案

二项式展开，留下最高次项

显然，若使得极限存在，则 得：

这是一个分割线~

考察函数的间断点 ​

设函数 ,则 的间断点是_____.

点击展开答案

一旦函数是用极限来定义的，那这个函数大概率是一个分段函数，所以要首先把函数表达式算出来

真
若 ==> f(x) = x^2

常数 ==> 抓大头
若 ==> f(x) = x - x^2

可得分段函数：

分析得：间断点为

考察中值定理算极限 ​

难度评级：⭐️⭐️

求极限

点击展开答案

法1:

左分式同除后通分，得：

由重要极限e得：

由拉格朗日中值定理，得：

介于和之间

可知，,对泰勒展开，得：

解得：

真是服了，两分钟写出来的题，对着手稿敲TeX，敲了10分钟才敲出来，当然也有部分原因是我对TeX还不是很熟悉，就比如我就需要去查一下才知道怎么打出来

推荐一篇，LaTeX公式总结文章👉️传送门👈️

这是一个分割线~

考察函数构造 ​

难度评级：⭐️⭐️
已知函数的定义域是，且满足，，求证：

点击展开答案

法1：

由且得：

我又悟了，我每天就精选1/2题放到网站上不就好了。

这是一个分割线~

考察复合函数泰勒展开求极限 ​

求极限

难度评级：⭐️⭐️

点击展开答案

法1：
对泰勒展开：

对泰勒展开：

原极限：

这是一个分割线~

考察极限相乘泰勒展开 ​

求当时，与为等价无穷小，则 ______. _____.

点击展开答案

对于
对于

可得：

考察费马定理+拉中 ​

难度评级：⭐️⭐️
函数在上有二阶导数，。若在上的最大值。证明：存在 ，使得。

点击展开答案

构造原函数：

需证，设存在使得
时，由费马定理知，。

由拉格朗日中值定理，得：

时
由拉格朗日中值定理，得：

得：

综上，得证：存在，使得

考察变上限求导 ​

alt text

点击展开答案

考察全微分 ​

设函数可微 且,,则 d

点击展开答案

观察题干给出的，仅有，可以对x求导

后半段过于复杂，先设为
代入：,得：

解得：

代入：,得：

解得：

解得：代入

考察二元函数最值 ​

求函数 在区域 上的最大值

点击展开答案

区域内部：
令

区域边界：

法1：Lagrange乘数法 注：目标函数转化
令

法2：极坐标（条件是：圆或椭圆）
需求在下的
令

法3：极坐标（不分边界和内部）
令求在时的最大值为

法4：均值不等式（不分边界和内部）

考察二重积分的极限 ​

知识点传送门
设 g(x) 有连续的导数, g(0)=0, g′(0)=a≠0, f(x,y) 在点 (0,0) 的某邻域内连续,则

点击展开答案

法1：（二重积分的积分中值定理）

抽象函数的二重积分 ​

设是可微函数的反函数，且 ,则的值

点击展开答案


考察抽象矩阵 ​

已知 , 又 , 则 _______.

点击展开答案

解得：

全面考察矩阵的运算技巧 ​

设是 5×4 矩阵，且的列向量线性无关是四阶矩阵，满足 2.是的伴随矩阵.则

点击展开答案

法1：
【秩不变口诀】
左乘列满秩（说明）

法2：
【AB=0】

有

法3：
【消除律】
左乘列满秩可消去

法4：

一定是方阵
【四秩相等】
可逆

法5：
【AB = 0的第二个角度】
的列向量是的解
只有零解
即的列向量都是零向量 ==>

【伴随的秩结论】
得：

考察线性相关性 ​

现有四个向量组
①
②
③
④
则下列结论正确的是
(A) 线性相关的向量组为①④; 线性无关的向量组为②③.
(B) 线性相关的向量组为③④; 线性无关的向量组为①②.
(C) 线性相关的向量组为①②; 线性无关的向量组为③④.
(D) 线性相关的向量组为①③④; 线性无关的向量组为②.

点击展开答案

选D

【线性相关性质】
（1）n+1个n维向量必相关
（2）低维无关，高维也无关

考察线性相关性2 ​

设 , , 都是 n 阶矩阵, 记向量组 (I) ; (II) ; (III) . 若向量组 (III) 线性相关, 则
(A) (I)、(II) 均线性相关.
(B) (I) 或 (II) 中至少有一个线性相关.
(C) (I) 一定线性相关.
(D) (II) 一定线性相关.

点击展开答案

法1：取行列式

或或

法2：反证法（取不了行列式）
假设：且
左列右行 ==> ==> AB线性无关与题设矛盾
否定假设：或

考察向量组表示 ​

(2021, 数农改) 若向量组 可由向量组 线性表出，则 线性无关是 线性无关的
(A) 充分必要条件.
(B) 充分不必要条件.
(C) 必要不充分条件.
(D) 既不充分也不必要条件.

点击展开答案

【线性表示结论】 （5）向量组可以表示向量组
<==>
==>

(2021, 数农) 设n维列向量组 线性无关，则n维列 向量组 线性无关的充分必要条件为( )
(A) 向量组 可由向量组 线性表示.
(B) 向量组 可由向量组 线性表示.
(C) 向量组 与向量组 等价.
(D) 矩阵 与矩阵 等价.

点击展开答案

大前提：n维列向量组 线性无关 ==>

考虑（A）
必要条件
举反例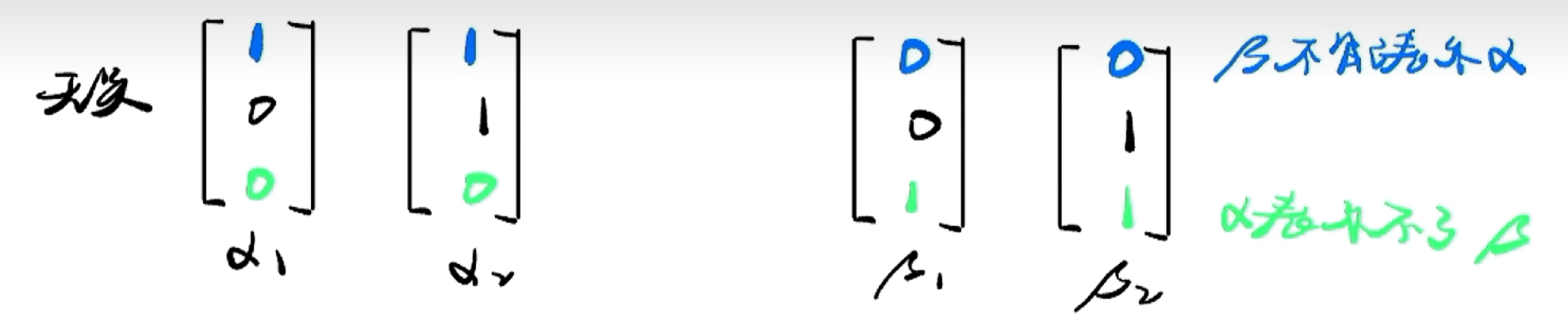： alt text
（A）（B）（C）都不是充分条件
排除（A）（B）（C）

（D）【矩阵等价】 ==>
大前提： 题干可翻译成：
大前提 + 题干 =
大前提 + 选项 =
显然是充分必要条件

考研真题 ​

分段积分，去绝对值 ​

难度评级：⭐️⭐️
设为正整数，记为曲线 与轴所围图形的面积，求，并求.

点击展开答案

法1：

对，你可以使用👉️行列式法👈️或者👉️表格法👈️，
解得：

由(2)带入(1)，得：

解得：

考察全微分 ​

设函数可微,且, , 则

点击展开答案

可先回顾这道题

代入：,得：

解得：

代入：,得：

解得：代入

考察二阶齐次特解 ​

【2016,数二】已知, 是二阶微分方程
的两个解.若,求,并与出该微分方程的通解.

点击展开答案

代入：
解得：

考察二维正态分布或相关系数公式 ​

【2022,数一】设随机变量 , 若在 的条件下, 随机变量 , 则 与 的相关系数为( )
(A) .
(B) .
(C) .
(D) .

点击展开答案

翻译条件：

法一：二维正态分布密度函数

==> ==> ==>

法二：相关系数公式



泊松积分 ==> ==> ==>

错题本 ​

高数 ​

空间曲线切线公式 ​

可微偏导问题 ​

二重定积分求和 ​

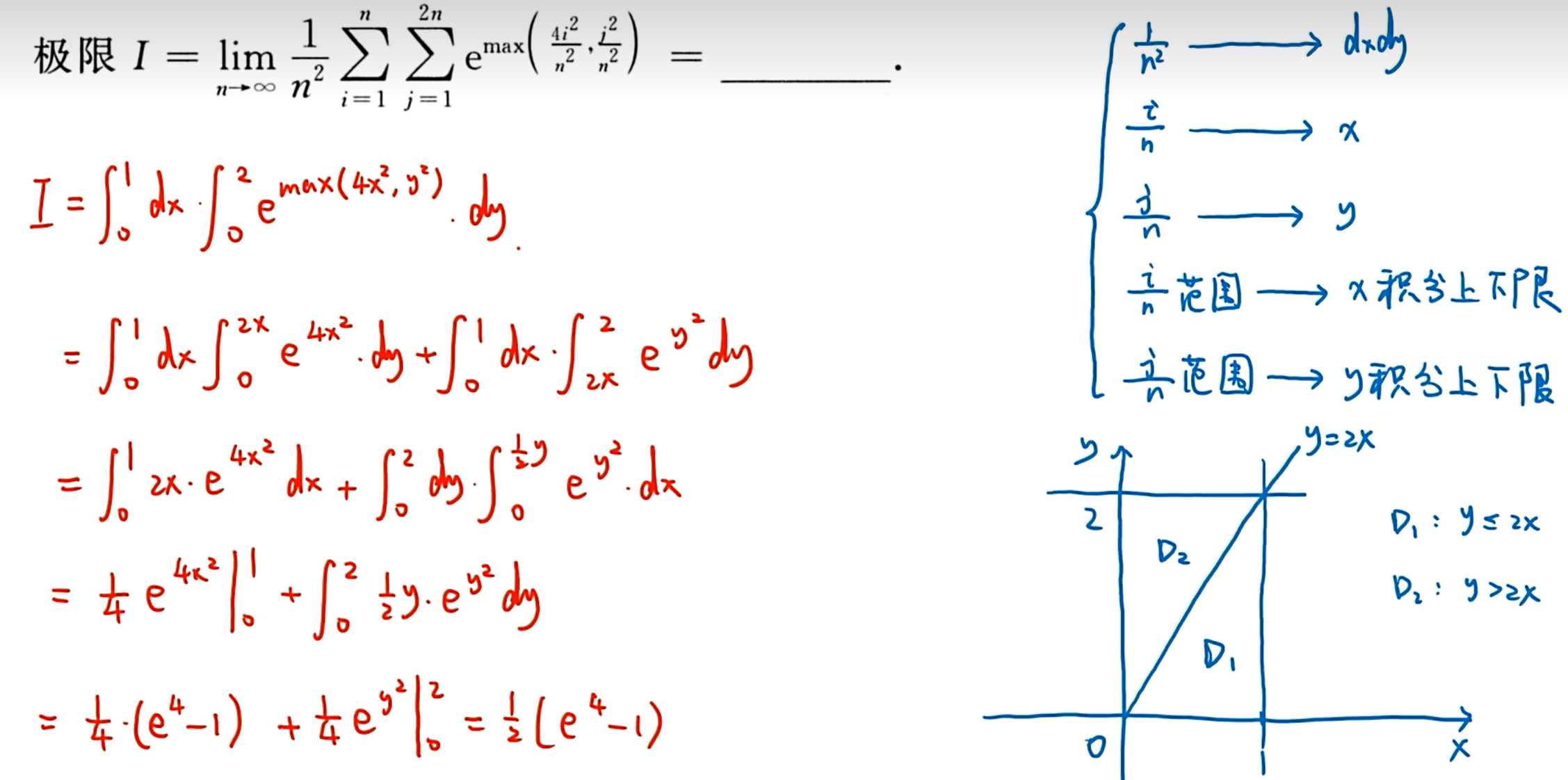
二类曲线参数化 ​

中值不等式问题 ​

偏导定义 ​

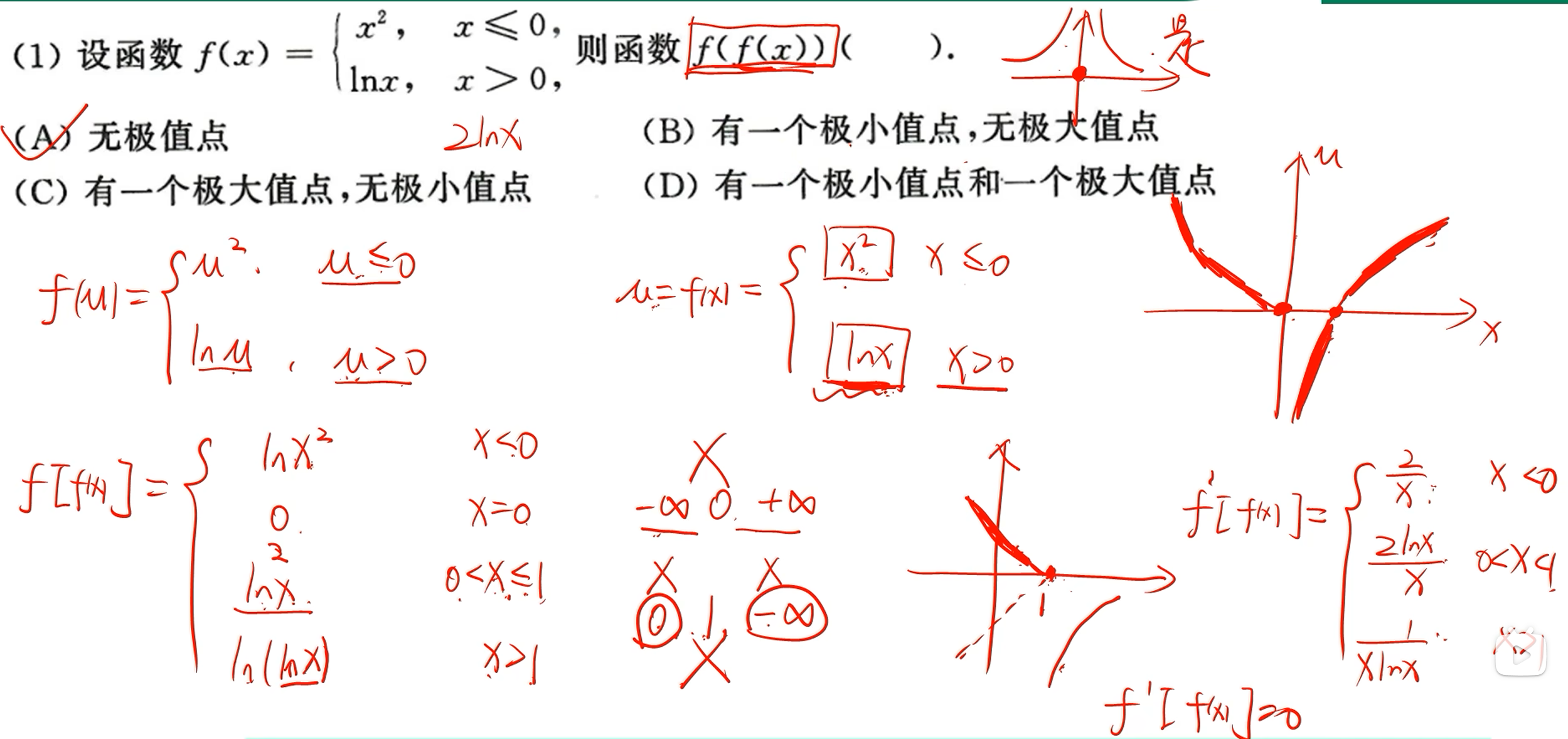
复合函数 ​

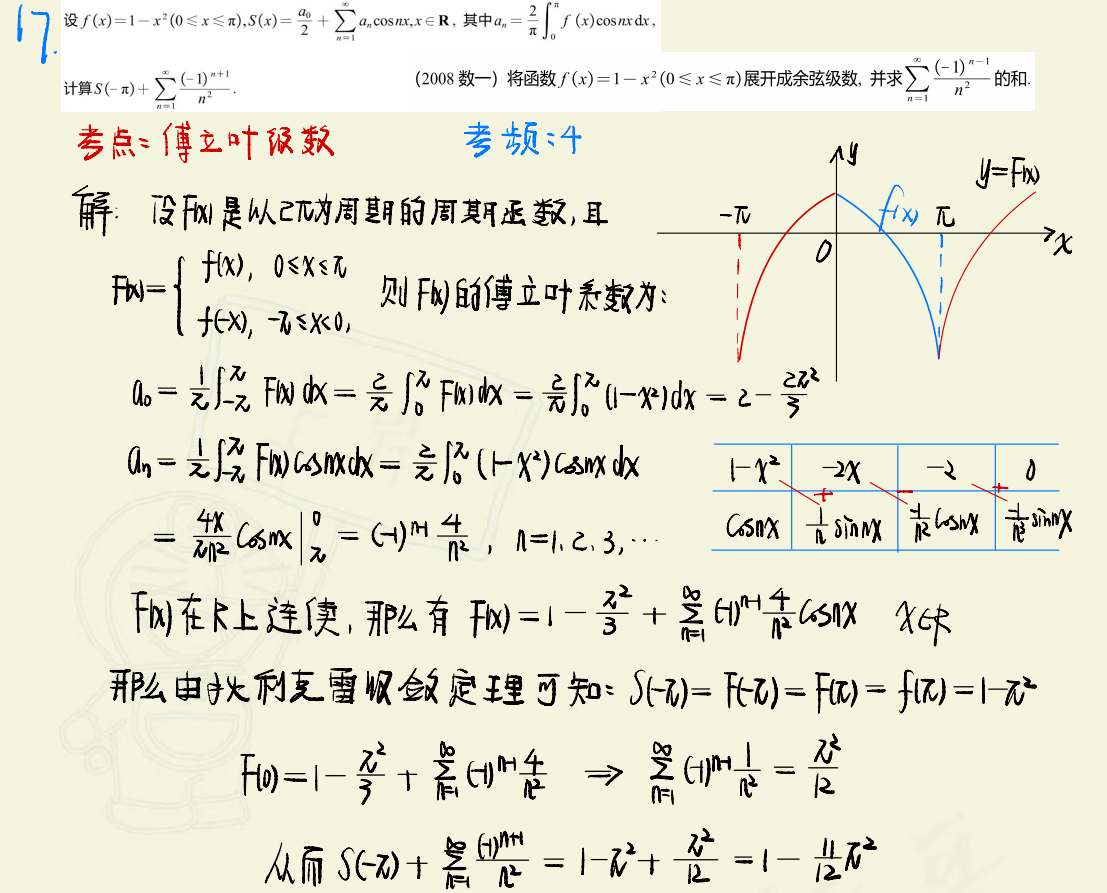
傅里叶级数 ​

洛必达 ​

奇偶性复合 ​

积分周期性 ​

线性代数 ​

普通正交矩阵 ​

AB=BA结论 ​

正定二次型结论 ​

​

矩阵方程化简（可逆分析） ​

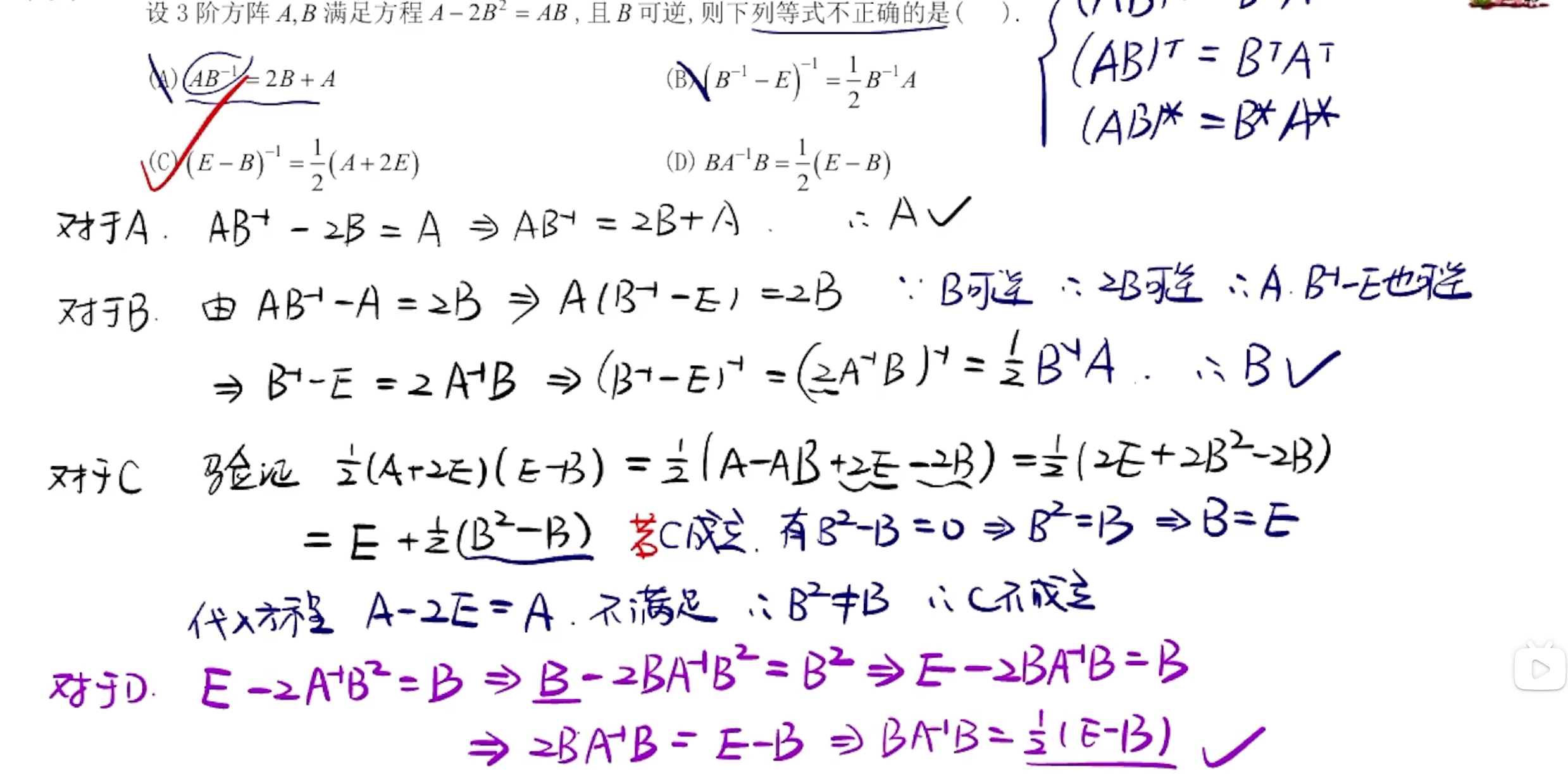
方程组同解 ​

方程组公共解 ​

正定与合同 ​

统计概率 ​

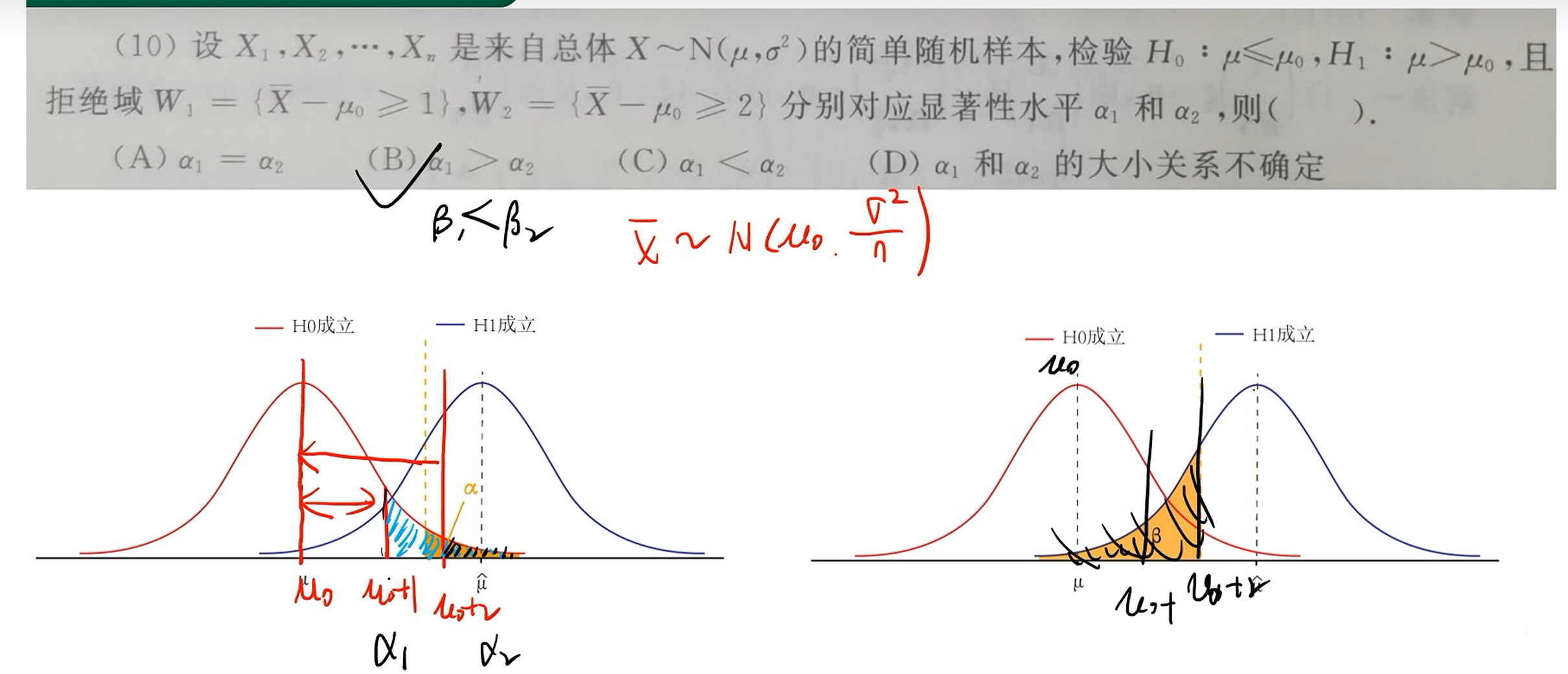
拒绝域 ​

离散似然函数 ​

设某箱中有 10 个产品，其中正品的个数为l.从中任取两个产品，记为两个产品中正品的个数，现对 独立观察三次，结果为1,2,2,则未知参数 的极大似然估计值

期望积分定义 ​

分布函数包含关系 ​

切绳问题 ​

两类错误（弃真取伪） ​

大数定律之一 ​

凑统二 ​

分布函数与最值函数 ​

拒绝域显著性水平 ​

经验之谈 ​

多元方程（等式） ​

等式中有多个参数，可尝试将一个参数设为变量，其他参数作为常数，进行求导

大部分公式，使用SimpleTex图片识别
在我看来，笔记是一个很好激活记忆的工具。
就比如学完一个知识点后，可能是一个月也可能是一周之后，对这个知识点的结论的印象变得模糊，所以重新翻看笔记就能够激活当时学习的情境，让我快速地重新掌握这个知识点。
但是其他人没有经历我当时学习的情境，所以部分细节无法理解或者没记上去的一些知识点没有掌握，导致不能够理解/学懂我的笔记内容。

为学日益,为道日损。——《道德经》
可以理解为，大量的信息日益增长，这些信息包括我们的实践经验，以及各种细碎的心得体会。而精炼的压缩过的概念、总结出来的原则日益削减。从而达到大道至简的境界。这一种封装与解压的关系，只有做到可以相互转换，我们的学习才能和谐。

Last updated:

Copyright@ 2024 daidai Shangguan